Гипотеза о симметричных простых близнецах

[Ryzl]

$\textbf{Гипотеза о симметричных простых близнецах}$

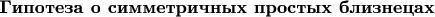
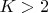
Пусть $K$ — любое чётное число, $K>2$. Тогда:
1. Существует множество пар простых чисел $(p,q)$, таких что
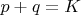
$p+q=K$ и $p=\frac{K}{2}-n$, $q=\frac{K}{2}+n$,
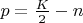
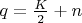
где $n$ — натуральное число, причём количество таких пар может быть больше одной.
2. Для каждого простого числа $p>p_0$ (для некоторого минимального порогового значения $p_0$)
существует хотя бы одно чётное число $K$, для которого
$p=\frac{K}{2}-n$,
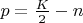
и
$q=\frac{K}{2}+n$,
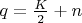
где $q$ — простое число, т.е. $p$ имеет симметричного простого близнеца $q$ относительно середины $\frac{K}{2}$

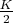
Эта гипотеза утверждает существование для каждого чётного числа пар простых чисел, симметричных относительно его половины, и для каждого простого числа в некотором диапазоне — существование соответствующего симметричного простого числа.

Тянет ли это на самостоятельную гипотезу?
Тестировал до 10^7 кандидатов (сначала наличие для четных чисел симметричных пар-близнецов простых чисел, затем для каждого простого числа наличие близнеца)
Тест до 10^7 прошел положительно.

Или это все таки тривиально и масло масленое? :)

[mihaild]

Если $p + q = K$, и $p, q$ - нечетные, то $n = \frac{K}{2} - p$ - целое, и $p = \frac{K}{2} - n$, $q = \frac{K}{2} + n$.
Так что первая часть - это просто утверждение, что все четные гэпы, большие двух, реализуются (что, скорее всего, правда, но вопрос открытый), а вторая - тривиальное следствие бесконечности простых.

[Ryzl]

mihaild в сообщении #1704003 писал(а):

Если $p + q = K$, и $p, q$ - нечетные, то $n = \frac{K}{2} - p$ - целое, и $p = \frac{K}{2} - n$, $q = \frac{K}{2} + n$.
Так что первая часть - это просто утверждение, что все четные гэпы, большие двух, реализуются (что, скорее всего, правда, но вопрос открытый), а вторая - тривиальное следствие бесконечности простых.

А использовать это для поиска простых чисел можно? Брать большое четное и искать около его половины? (в тесте расхождение с серединой было не более 77)

[mihaild]

Ryzl в сообщении #1704004 писал(а):

Брать большое четное и искать около его половины?

Поскольку любое число это половина четного, то чем это отличается от просто "искать где придется"?

[wrest]

Ryzl в сообщении #1704000 писал(а):

Пусть $K$ — любое чётное число, $K>2$. Тогда:
1. Существует множество пар простых чисел $(p,q)$, таких что
$p+q=K$

Так это же не доказано (проблема Гольдбаха)

[Dmitriy40]

Ryzl в сообщении #1704004 писал(а):

(в тесте расхождение с серединой было не более 77)

А это и не может быть больше половины максимального интервала между простыми числами, который для чисел до 17млн равен 154. Так что да, тыкнув в произвольное число до 17млн, не далее 154/2=77 в любую сторону от него найдётся простое. А если тыкать в числа до 18361375334787046697, то простое будет не далее 1530/2=765 от него.

[Ryzl]

wrest в сообщении #1704006 писал(а):

Ryzl в сообщении #1704000 писал(а):

Пусть $K$ — любое чётное число, $K>2$. Тогда:
1. Существует множество пар простых чисел $(p,q)$, таких что
$p+q=K$

Так это же не доказано (проблема Гольдбаха)

Вот и я про тоже )

И этих пар оочень много получилось у меня. (по крайней мере при тестировании до 10^7)

[Ryzl]

Не обнаружил ли я еще одно множество простых чисел?

Т.е. все простые числа меньше некоторого четного числа разбиваются на два множества:
1. Простые числа имеющие симметричного (относительно половины четного числа) близнеца
2. И простые числа не имеющие симметричного близнеца

[Ryzl]

Вот такая картина вырисовывается. Зависимость K(n)

[EUgeneUS]

Ryzl в сообщении #1704321 писал(а):

относительно половины четного числа

Какой изысканный способ сказать "относительного любого числа"

[Dmitriy40]

Мне теперь интересно какие же два простых не симметричны относительно половины некоего чётного числа? Ведь для любых простых $p,q$ больших $2$ число $K=\frac{p+q}{2}$ будет центром симметрии исходных $p,q$ и вдвое меньше чётного числа $2K$.

Ryzl в сообщении #1704321 писал(а):

2. И простые числа не имеющие симметричного близнеца

Так какая пара простых не симметрична или какое простое не имеет симметричной пары? Покажите плиз.

[Ryzl]

Т.е. то что вокруг любого числа существуют симметричные простые близнецы это тривиально. И сумма этих двух симметричных простых близнецов будет равна некому четному числу это не доказательство гипотезы Гольдбаха?
У любого четного числа есть середина (половина), вокруг этой середины всегда существуют не менее одной пары симметричных простых близнецов дающих в сумме это любое четное число.

[Dmitriy40]

Ryzl в сообщении #1704764 писал(а):

Т.е. то что вокруг любого числа существуют симметричные простые близнецы это тривиально.

Тривиально обратное утверждение: для любых двух простых есть центр их симметрии, равный половине их суммы.
Но вот что для любого чётного числа всегда найдутся два симметричных простых - нет, уже не тривиально.

[wrest]

Ryzl в сообщении #1704764 писал(а):

И сумма этих двух симметричных простых близнецов будет равна некому четному числу это не доказательство гипотезы Гольдбаха?

Да нет же. Из гипотезы Гольдбаха следует утверждение этой темы, и это следование - школьная арифметика.
Вы заблудились в двух соснах школьной арифметики.
Чтобы сумма двух чисел вышла чётной, оба слагаемых должны иметь одинаковую четность.
В случае простых слагаемых это означает что они оба нечётны кроме случая $2+2=4$
Два любых нечётных числа "симметричны относительно их полусуммы" - это тривиальное школьное утверждение, вокруг которого вы хотите сделать открытие
То есть: два любых простых нечётных числа "симметричны" относительно их полусуммы. И вообще, два любых нечетных числа (в том числе два любых простых нечетных числа) являются "симметричными близнецами".
Так что

Ryzl в сообщении #1704000 писал(а):

это все таки тривиально и масло масленое

и прямо следует из бинарной гипотезы Гольдбаха. Доказывайте сперва её

[Ryzl]

Давайте сначала.
1. Вокруг каждого числа есть симметричные простые близнецы (более одной пары).
2. Каждое число есть половина четного числа.

Следовательно любое четное число есть сумма двух простых чисел.

Что не так?