Насколько я понимаю, из каждой модели

ZF можно сделать подмодель

(конструктивный универсум), которая будет моделью ZFC.
Да, так и есть. Кроме того, в конструктивном универсуме будет выполняться и обобщённая континуум-гипотеза [GCH] независимо от того, выполнялась ли она в исходной модели. Вообще, конструктивный универсум — наименьший, содержащий все ординалы, в котором выполняются аксиомы ZF.
Интересно, что аксиома выбора является следствием обобщённой континуум-гипотезы
Кстати, здесь множества "конструктивные" не в том смысле, как в конструктивной математике; может быть, их следовало бы называть определимыми.
Вкратце идея в следующем. Для множества

обозначим через
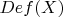
совокупность всех множеств
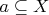
, которые можно определить формулами теории множеств с параметрами из множества

. Тогда определяем множества

индукцией по всем ординалам

:
1)
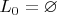
;
2)
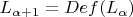
;
3)
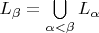
, если ординал

предельный.
Конструктивным универсумом называется класс
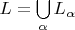
, где объединение берётся по всем ординалам.
Подробности нужно смотреть в литературе.
Справочная книга по математической логике. Часть II. Теория множеств. Москва, "Наука", 1982.
Глава 5. Конструктивность.