Пентадекатлон мечты

[EUgeneUS]

Dmitriy40 в сообщении #1706504 писал(а):

Единственно, хотелось бы ещё потом посмотреть на паттерны с $5^5, 7^5, 11^5, 13^5$ - они все снижают lcm за счёт уменьшения количества добавляемых квадратов простых, вдруг это интересно ..

Запутались мы. Не уменьшают количества добавляемых квадратов простых паттерны с $5^5, 7^5, 11^5, 13^5$
$5, 7, 11, 13$ как не впихивай в 21 позицию, может быть только одно место со степенью больше 1. И туда выгодно ставить квадрат. Пятая степень также убирает один квадрат, но жрёт одно простое в множителях.

Есть ещё нюанс с искусственным повышением количества $pqr$.
Я рассматривал на калькуляторе шансов паттерны с искусственным повышением количества $pqr$ путем умножения на простое в местах $pqrs$. Нет выигрыша, один проигрыш. А там подставлялись числа меньше 100. Поэтому этот финт с заменой $5^2 \to 5^5$ с целью увеличить количество $pqr$ за счет $pqrs$ точно не сработает.

А с тройкой другая история. Её можно впихнуть так, что будет три места со степенью больше 1. Три квадрата туда поставить нельзя, поэтому ставим два квадрата и $3^5$.

8 - минимальное количество подставляемых простых в квадрате.
Не рассматриваем $5^5, 7^5, 11^5, 13^5$.

[EUgeneUS]

Для информации считающим.
Расчет по паттерну 0-3-16-2(8) с 8! перестановками:
до 1e47 даст шансы найти цепочку 0,57%
до 1e48 даст шансы найти цепочку 4,29%
до 1e49 даст шансы найти цепочку 28,54%
до 1e50 даст шансы найти цепочку 92,47%
до 1,182e50 даст шансы найти цепочку 95,00%

-- 20.10.2025, 19:57 --

Первая valids=18 в паттерне 0-3-16-2(8).
Время от начала расчета примерно 12-14 часов.
Вроде бы самая малая из известных.

(Оффтоп)

185-15580   33317375471164112126448417286147458736599281169   b1111 111 1 1111111111e      18   [4, 1, 6, 8, 2, 5, 7, 3]

[Dmitriy40]

EUgeneUS в сообщении #1706556 писал(а):

Вроде бы самая малая из известных.

Не, моя на порядок меньше.

-- 20.10.2025, 22:08 --

EUgeneUS в сообщении #1706556 писал(а):

Для информации считающим.

Печально.

[Yadryara]

$\tikz[scale=3, transform shape, font=\fontsize{11}\selectfont, black!70!]{ \node at (4.79,10)[shading=ball,ball color=green!70!violet!100!, white] {\color{yellow}\Huge\textbf{21}} }$

$\tikz[scale=.71, transform shape, font=\fontsize{11}\selectfont, black!70!]{ \node at (4.79,10)[shading=ball,ball color=red!70!violet!100!, white] {\color{yellow}\Huge\textbf{52556626259340931919271848023566857910792017169}} }$

[Huz]

Yadryara в сообщении #1706582 писал(а):

52556626259340931919271848023566857910792017169

Congratulations - also a new upper bound for D(48,19) and D(48,20). :)

[EUgeneUS]

Yadryara
Поздравляю!

Насколько понимаю, нашлась в 0-3-16-2(8) с 8! перестановками.
Интересно, в прямом или зеркальном?
Если в зеркальном, то шансы были чуть больше процента ($2 \cdot 0.57$).

[Yadryara]

Спасибо, друзья Спасибо за разностороннюю помощь.

А Huz-то оказывается за темой следит, но молчит как партизан

EUgeneUS в сообщении #1706589 писал(а):

Насколько понимаю, нашлась в 0-3-16-2(8) с 8! перестановками.
Интересно, в прямом или зеркальном?

Эту инфу можно очень легко получить из самого числа. В прямом.

Да, я действительно вчера в 17:47 запустил на пробу 1-й зеркальный комплект. И долго ничего не находилось Потом, уже где-то в 18:50-57, увидел что 2 приближения всё-таки нашлись. И... меня сморило. Заснул с включённым светом. Проснулся за полночь. И по логам установил что 21-ка нашлась через полчаса как я отрубился, в 19:26.

Но счёт не был прекращён и я все потоки досчитываю и статистику опубликую.

-- 21.10.2025, 07:32 --

Yadryara в сообщении #1706479 писал(а):

Считаю, кстати, в основном выше, до 1e48.

Кстати, вот сейчас стал разбираться, оказывается я перепутал. Я указал st=435920 и получались в основном 47-значные числа. Но, хотя выше уже делал аналогичную ошибку, я опять почему-то думал, что 47-значные это до 1e48, а они, оказывается, до 1e47.

[VAL]

Yadryara в сообщении #1706582 писал(а):

$\tikz[scale=3, transform shape, font=\fontsize{11}\selectfont, black!70!]{ \node at (4.79,10)[shading=ball,ball color=green!70!violet!100!, white] {\color{yellow}\Huge\textbf{21}} }$

$\tikz[scale=.71, transform shape, font=\fontsize{11}\selectfont, black!70!]{ \node at (4.79,10)[shading=ball,ball color=red!70!violet!100!, white] {\color{yellow}\Huge\textbf{52556626259340931919271848023566857910792017169}} }$

Поздравляю!

Yadryara, в нужные места в OEIS внесете изменения?
К сожалению, право править 1-ю страницу тему у меня изъяли
Так что, подготовлю обновление и попрошу опубликовать. Заодно просуммирую все локальные достижения текущего года.

Не верил я в шаблоны (паттерны) без простых... Был не прав.

Судя, по затраченному времени 22 не за горами.

[EUgeneUS]

Yadryara в сообщении #1706590 писал(а):

В прямом.

Значит и у меня найдётся в ближайшие сутки. А если бы не моргнул свет позапрошлой ночью, то уже бы и нашлась

-- 21.10.2025, 08:07 --

VAL в сообщении #1706592 писал(а):

Судя, по затраченному времени 22 не за горами.

Не знаю, не знаю... Тут очень малые шансы сыграли. Всё время так везти не может.

(Оффтоп)

Лет 10 назад пришел в незнакомую компанию поиграть в покер. И в первый же вечер собрал флеш-рояль.
Потом с этой компанией регулярно играли 10 лет, никто флеш-рояль не собрал за это время.
Так что бывает, малые шансы играют. Но редко

Посмотреть на $D(48,22)$ это не мешает, конечно.

ИМХО, другие улучшения будут более перспективны. Можно посмотреть на 36 делителей - там два шага до финала. Или на 24 делителя. Многие цепочки с 12n делителей можно попытаться улучшить.

Для 12(2n+1) выбор хороших паттернов ограничен, и скорее всего уже использовали эффективные. Там есть вариант очень сильно увеличить количество паттернов. Но как для огромного количества паттернов делать ускорители?
А вот для 24n можно поподбирать эффективные паттерны через калькулятор шансов.

[VAL]

Обновил инфу здесь.

И, чтобы два раза не вставать:
$M(480) \ge 10$

(Начало цепочки)

n = 1577962800669647101534495708122553567748720220696181852003131495765225057327359770620

Числа в цепочке 84-значные. Но удалось найти, не прибегая к Alpertron'у и прочим YAFU.

[Yadryara]

VAL в сообщении #1706592 писал(а):

Yadryara, в нужные места в OEIS внесете изменения?

Попытался внести в две:
A006558 и A119479.

EUgeneUS в сообщении #1706593 писал(а):

А если бы не моргнул свет позапрошлой ночью, то уже бы и нашлась

Я уже говорил: надо было просто продолжить примерно с того же места. Дмитрий выше рассказывал как.

[EUgeneUS]

EUgeneUS в сообщении #1706593 писал(а):

Для 12(2n+1) выбор хороших паттернов ограничен, и скорее всего уже использовали эффективные. Там есть вариант очень сильно увеличить количество паттернов.

На примере $D(36,15)$

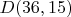
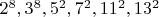
1. Для паттернов со структурой $2^8, 3^8, 5^2, 7^2, 11^2, 13^2$ количество подставляемых квадратов простых: 19.
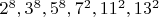
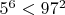
2. Для паттернов со структурой $2^8, 3^8, 5^8, 7^2, 11^2, 13^2$ количество подставляемых квадратов простых: 18. Но $5^6 < 97^2$. Эти хуже.
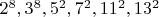
3. Для паттернов со структурой $2^8, 3^8, 5^2, 7^2, 11^2, 13^2$ минимальное количество простых - 10, остальные pq.
4. Итого, оптимальный тип паттерна 10-5(19). Все они имеют структуру степеней $2^8, 3^8, 5^2, 7^2, 11^2, 13^2$.
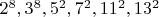
5. Всего таких "батчей" (до расстановки простых) нашлось 1343 штуки (число нечётное, почему-то. Возможно, один пропустил).
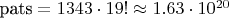
6. Итого всего паттернов такого типа: $\text{pats} = 1343 \cdot 19! \approx 1.63 \cdot 10^{20}$. Это настолько дофига, что нам вообще не нужно делать итерации внутри паттерна, достаточно перебирать собственно паттерны.

7. Числа будут искаться в районе $1...10 \cdot 10^{45}$.

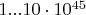
-- 21.10.2025, 10:37 --

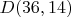
Для $D(36,14)$ количество подставляемых квадратов простых уменьшится на 2 до 16.
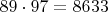
LCM уменьшится в $89 \cdot 97 = 8633$ раза.
Сколько будет минимальных простых, не знаю. На одно - точно. Можно ли ещё меньше - не знаю.
А вот количество подходящих "батчей" (паттернов до расстановки простых в квадрате) даже увеличится.
То есть опять - перебор внутри паттерна не требуется, нужно перебирать паттерны.

-- 21.10.2025, 11:04 --

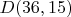
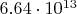
Для $D(36,15)$ калькулятор шансов говорит, что при поиске чисел в $10^{46}$ (если тут ошибся, нужно будет пересчитать, конечно) нужно проверить по одному кандидату в $6.64 \cdot 10^{13}$ паттернов, что сильно меньше $19!$. При заданной вероятности найти цепочку 0.95.

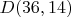
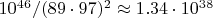
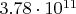
Для $D(36,14)$ калькулятор шансов говорит, что при поиске чисел в $10^{46} / (89 \cdot 97)^2 \approx 1.34 \cdot 10^{38}$ (если тут ошибся, нужно будет пересчитать, конечно) нужно проверить по одному кандидату в $3.78 \cdot 10^{11}$ паттернов, что сильно меньше $18!$. При заданной вероятности найти цепочку 0.95. (UPD: тут поправил).

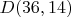
Вот для такого батча считал. Для $D(36,14)$ просто обрезается последняя позиция.

#;1;2;3;4;5;6;7;8;9;10;11;12;13;14;15
b18483:;3^8;2.7^2;13^2;2^2.3;5;2.11^2;3;2^8;7;2.3^2.5^2;.;2^2;3;2;5
v=;6561;98;169;12;5;242;3;256;7;450;1;4;3;2;5
sq1;1;83;79;73;71;67;61;1;41;1;59;43;53;47;89
sq2;1;1;1;1;17;1;19;1;37;1;23;1;29;31;97
M=;6561;675122;1054729;63948;7284245;1086338;4029843;256;16109023;450;1841449;7396;7087107;4245698;372643445
p/pq;pq;p;pq;p;p;p;p;pq;p;p;pq;pq;p;p;p

-- 21.10.2025, 11:20 --

Ах, да. Оценки весьма примерные. Статистику не собирал. Но в плюс-минус полпорядка должен попасть.

[EUgeneUS]

EUgeneUS в сообщении #1706601 писал(а):

Для $D(36,14)$ количество подставляемых квадратов простых уменьшится на 2 до 16.
LCM уменьшится в $89 \cdot 97 = 8633$ раза.

В $(89 \cdot 97)^2 = 74528689$ раза.

[Dmitriy40]

Yadryara
Поздравляю!
Удивительно как срабатывают столь малые шансы.
Да ещё и на паттерне без простых (т.е. с более медленной проверкой). И ведь на чистом PARI.

[VAL]

Yadryara в сообщении #1706595 писал(а):

Попытался внести в две:
A006558
и A119479.

Модераторы отозвались?

Я правильно понимаю, что наиболее перспективный шаблон на 22-ку не должен содержать простых и должен как можно больше $pqr$?