Ради интереса проверил вероятности степеней больших (больше 100) делителей для миллиона случайных чисел в диапазоне 1e19-1.8e19. Получилось следующее:
Опять хорошо забытое старое.
Мы уже делали подобную статистику. Причем не для произвольных чисел, а для тех, которые возникают в наших алгоритмах.
В этой теме упомянутая статистика где-то выложена.
И картина там принципиально иная.
Можно поискать точные значения, но по памяти скажу, что с отрывом наиболее популярны случаи

и

.
Далее идут

и
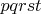
и только потом

.
Размеры исследуемых чисел были существенно больше, 30-40 знаков.
Картина для 30-значных и 40-значных схожа. Хотя с ростом чисел мода ожидаемо мигрирует от

к

.
-- 27 сен 2025, 16:18 --То что выкладывалось здесь, пока не нашел (многовато пишем

)
Но аналогичную статистику я проводил перед поиском достаточно длинных цепочек для каждого

.
Вот, например, для 17 чисел по 96 делителей:
Код:
[7.350000, 22.64000, 29.67000, 23.38000, 11.93000, 3.840000, 1.190000]
Здесь слева направо процент:
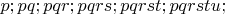
более 6-и простых.
Проверяемые числа имеют по 48 знаков.
Картина немного отлична от той, что я вспомнил. По-видимому, это связано с тем, что для

в шаблоне участвует мало фиксированных простых. Или просто память подвела
 -- 27 сен 2025, 16:30 --
-- 27 сен 2025, 16:30 --PS:
Уточнение.
Это статистика не для цепочек длины 17, а для цепочек длины 10. Соответственно числа 30-значные и список фиксированных модулей меньше.
Просто в программку для длинных цепочек она перекочевала по наследству
