Пентадекатлон мечты

[VAL]

Пентадекатлон мы нашли для шаблона с 11-ю простыми.
То есть для ускорителей - это не помеха. А возможно, наоборот.
Тогда, не исключено, что цепочку из 21-го числа лучше искать не для $k=48$, а для $k=24$.
Сделал табличку на 9 простых. (Для $k=48$ без "костылей", увеличивающих перебираемые числа и уменьшающих вероятность, больше 5-и простых не получается.)

[Dmitriy40]

Разница между 53 (M48n20) и 45 (M24n18) цифрами в плане разложения несущественна, зато почему-то M48 известна длиннее ... Подозреваю на большее количество делителей раскладывать заметно проще (и вероятнее).
Но можно и М24 посмотреть.

-- 25.09.2025, 20:58 --

VAL в сообщении #1703250 писал(а):

Пентадекатлон мы нашли для шаблона с 11-ю простыми.
То есть для ускорителей - это не помеха. А возможно, наоборот.

Помнится M36n13 с 9-ю числами нашли влёт, чуть ли не за дни, а вот M36n15 с 11-ю числами я за пару недель не нашёл кандидатов даже близко, так что только это не показатель, зависимость сложнее.

[EUgeneUS]

Dmitriy40 в сообщении #1703252 писал(а):

Помнится M36n13 с 9-ю числами нашли влёт, чуть ли не за дни,

Там какое-то везение оказалось. Удача.
Когда-то должна была сработать, чисто статистически

[Dmitriy40]

VAL в сообщении #1703250 писал(а):

Для $k=48$ без "костылей", увеличивающих перебираемые числа и уменьшающих вероятность, больше 5-и простых не получается.

Не понял, у меня же получилось на 9 чисел, при этом разместить надо простые по 47. Про костыли не знаю.

-- 25.09.2025, 21:40 --

А для M24n31 можно сделать до 17 проверяемых чисел, из которых 12 сразу, а ещё 5 размещая квадраты простых 31-47.
Минимально же одно проверяемое число, без дополнительных простых более 29 (правда тут аж 5 искомых простых в квадрате! Мрак!).

[VAL]

Dmitriy40 в сообщении #1703254 писал(а):

VAL в сообщении #1703250 писал(а):

Для $k=48$ без "костылей", увеличивающих перебираемые числа и уменьшающих вероятность, больше 5-и простых не получается.

Не понял, у меня же получилось на 9 чисел, при этом разместить надо простые по 47. Про костыли не знаю.

Не знаю.
Те шаблоны (мне это слово категорически больше нравится, чем "паттерн"), что Вы прислали, во-первых, рассчитаны на 31 число, а не на 21. А во-вторых, в каждом из них стоят больше десятка чисел, свободных от квадратов. Это означает, что оставшиеся множители в цепочке должны делиться на квадраты (не говоря уже о том, что в первом одно просто должно быть квадратом). А квадраты всех маленьких чисел у нас уже заняты. Поэтому практический шанс найти цепочку по Вашим паттернам - ноль (или я чего-то не понимаю).
В моих же таблицах каждый оставшийся множитель либо простое число, либо произведение различных простых. Вероятность такого события для одной позиции в десятки или сотни раз выше. А для всей цепочки...

По поводу "костылей". Чтобы долго не объяснять прикладываю таблицу, где они использовались для поиска цепочки из 10 чисел по 336 делителей.
Там 3 костыля позволяют начинать поиск с проверки на простоту.

[Dmitriy40]

VAL в сообщении #1703257 писал(а):

А во-вторых, в каждом из них стоят больше десятка чисел, свободных от квадратов. Это означает, что оставшиеся множители в цепочке должны делиться на квадраты (не говоря уже о том, что в первом одно просто должно быть квадратом). А квадраты всех маленьких чисел у нас уже заняты. Поэтому практический шанс найти цепочку по Вашим паттернам - ноль (или я чего-то не понимаю).

Я специально не стал расставлять квадраты на те места, где они не приводят к появлению проверяемых чисел - ведь это можно сделать в любом порядке, который уже на ни что не влияет, только LCM (и шаг перебора) увеличивает.

-- 25.09.2025, 22:30 --

Проверил 100 тысяч случайных чисел с 48 делителями в диапазоне 1e19-1.8e19, из них 86% содержат максимум квадрат, 6% содержат куб, 7.7% содержат 5-ю степень, 7-ю и 11-ю степень содержат менее 0.1% чисел.

[VAL]

Dmitriy40 в сообщении #1703260 писал(а):

Я специально не стал расставлять квадраты на те места, где они не приводят к появлению проверяемых чисел - ведь это можно сделать в любом порядке, который уже на ни что не влияет, только LCM (и шаг перебора) увеличивает.

Конечно, все так. Но если этих квадратов не будет, вероятность, что они или другие квадраты появятся случайно, мизерна.

Dmitriy40 в сообщении #1703260 писал(а):

Проверил 100 тысяч случайных чисел с 48 делителями в диапазоне 1e19-1.8e19, из них 86% содержат максимум квадрат, 6% содержат куб, 7.7% содержат 5-ю степень, 7-ю и 11-ю степень содержат менее 0.1% чисел.

Понятно, что числа, имеющие по 48 делителей обязаны делиться на квадрат или большУю степень.

-- 25 сен 2025, 23:33 --

У меня стойкое deja vu, что все это мы уже обсуждали с теми же аргументами три с половиной года назад.

[VAL]

Небольшая разминка перед большой факторизацией.

(Два числа)

120102431242479962100699518697405381339463910368961485981143247040815969307329596136075985061025913519474634712316244115858719042425311 (135 digits)
1259510998720995010311080583484144213061685053612820263322759166932557063456356255963662508649690144370472919552083251419685692486742058289 (139 digits)

Если первое распадется на два простых множителя, второе не нужно.
Если второе распадется на три простых множителя, первое не нужно.

Наконец, если первое распадется на три, а второе на два простых, не нужны оба, будем искать другие

PS: Похоже, все идет к третьему случаю
Первое число распалось на три сомножителя

[Dmitriy40]

Обнаружил у себя ошибку в программе генерации паттернов/шаблонов (вместо $3^3$ клался лишний $2^2$) и потому мои слова выше наверняка ошибочны, надо всё пересчитывать.

[EUgeneUS]

А есть ли какие-то оценки для вероятностей вида

$$P(N, k, l, m ...)$$

Где $N$ - число
$k$ - количество простых в первой степени в факторизации
$l$ - количество простых в квадрате в факторизации
$m$ - количество простых в кубе в факторизации
и т.д.

То есть $P(N, 3, 1, 0, 0 ...)$ - это вероятность, что факторизация числа $N$ будет иметь вид $pqrs^2$.

Может какие-то статьи известные есть?
Это просто обобщение вопроса о плотности простых чисел: $P(N, 1, 0, 0 ...)$ - вероятность, что числе $N$ окажется простым.

[VAL]

Ответ на вопрос из другой темы, который более уместен здесь.

Yadryara в сообщении #1703202 писал(а):

Для цепочек длиной от 10 с 12-ю делителями обязательным было число $32p$. А нет ли аналогичного обязательного числа для длинных цепочек с 48-ю делителями?

Нет. Обязательным будет одно из чисел $32pqr, 32p^3q, 128p^2q, 2042pq, 8388608p$.
И еще несколько фантастических (в отличие от перечисленных) вариантов, в которых нет простого числа в первой степени.

-- 26 сен 2025, 09:16 --

EUgeneUS в сообщении #1703282 писал(а):

А есть ли какие-то оценки для вероятностей вида

$$P(N, k, l, m ...)$$

[..]

Частные случаи безусловно изучены. Например, хорошо известна асимптотика чисел свободных от квадратов.
Но дело в том, что даже если есть ответ на Ваш вопрос в общем виде, для нашей задачи он не применим.
Наличие простых множителей в фиксированных степенях у нашего числа и его соседей искажает картину.

[VAL]

(Идем на рекорд?)

102854360885650221107443682427837181590726098865302566597414093088630571352766838563182468345201699890467357797889043949477766057034678611077378794086293031 (156 digits)
170440964358202509659188028465887388932283440163512404713384793635082141512085419670031246136184337231068558908440810910358237180203660687979193297492088772076595471934380039535731 (180 digits)

Разложение первого числа на ДВА простых даст восьмерку для $k=7128$. Аналогичный эффект даст разложение второго числа на ТРИ простых.

[DemISdx]

VAL в сообщении #1703286 писал(а):

разложение второго числа на ТРИ простых

VAL в сообщении #1703286 писал(а):

Разложение первого числа на ДВА простых даст восьмерку

Понял.
Второе число уже в работе, как раз до понедельника наверняка хватит, а может и поболее будет.
А первое попозже запущу, но планирую сегодня.

[DemISdx]

VAL в сообщении #1703265 писал(а):

если первое распадется на три, а второе на два простых, не нужны оба, будем искать другие

Похоже третий вариант...

(Результат по 12595...)

NFS elapsed time = 26124.9893 seconds.
Total factoring time = 28980.2687 seconds


***factors found***
P61 = 7770644550612203849755973255506804246972781961041906019249013
P78 = 162085782011707828094235190794136390775389139470677898492598795222489064466253

***factorization:***
1259510998720995010311080583484144213061685053612820263322759166932557063456356255963662508649690144370472919552083251419685692486742058289=7770644550612203849755973255506804246972781961041906019249013*162085782011707828094235190794136390775389139470677898492598795222489064466253

Разминка завершена.
Запустил 10285... (т.е. первое из рекордных)

[Huz]

Hi all, I just got informed that this thread is alive again, I hope you didn't miss me too much. :)

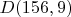
I've hardly touched the code since we last spoke, but I continue to do runs to improve known bounds (mostly very long runs now); I have not updated the OEIS entry for a while - I have a bunch of data to extend the a-file up to $n=200$ or $n=250$, so please let me know of any improvements you find in that range. (I've grabbed VAL's recent result for $D(156,9)$ already.)

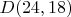
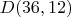
I'm currently have threads working to show $D(48,10)$ is minimal (which will take another year or two), and to reduce smallest known values for $D(24,18)$ and $D(36,12)$. I can confirm the recently posted list of best known values for D(48,k) match my latest data.

Unfortunately a stupid slip of the mouse a few months ago caused me to lose a bunch of notes and helper code that were not checked in to git (including the code I used to generate the OEIS data file, with all the information on who found which result and when), so the next update will involve a lot of manual effort.