Пока я писал Вам ответ на Ваши вопросы и высказывания об атоме на предыдущей странице (да, решил-таки написать), вижу, что Вы уже добавили здесь существенные пояснения. Так что, похоже, мой текст уже не нужен; если Вы всё основное знаете. Но теперь мне жалко его выбрасывать
. Поэтому, с извинениями за возможную его никчёмность, всё-таки вот он:
речь именно о состояниях единственного во Вселенной атома водорода с разными значениями энергии.
Плевать на интерпретации. Я вижу, что в состоянии с неопределённой энергией осциллируют плотности зарядов и токов, что означает неизбежное взаимодействие с электромагнитным полем, так что электрон в этом состоянии вечно оставаться не может.
Кванты - это теория про состояния систем и их эволюцию. И я задаю вопросы про состояния систем и их эволюцию, а не про то, что увидит какой-то воображаемый наблюдатель.
Комментировал я это в обратной последовательности:
"Кванты", если говорить только о проверенной опытом теории, являющейся "рабочей лошадкой" у физиков, занятых задачами практики, а не философией, это теория про вероятности и средние значения разнообразных физических величин, характеризующих системы.
Волновые функции

в этой теории служат одним из средств вычислений вероятностей и средних значений физ. величин, наряду с ещё одним важным средством вычислений - с операторами. Объектами вычислений операторы и волновые функции в теории являются, а объектами наблюдения в опыте - нет. Наблюдать

для одного экземпляра системы невозможно. В терминах "вероятность" и "среднее значение" в рабочей квантовой теории всегда подразумевается статистический ансамбль, даже если это не говорится явно.
Если в задаче решено учитывать взаимодействие электрона с электромагнитным полем, как с квантовой системой, то это надо делать сразу, а не так, что сначала пишем

для электрона без поля, а потом вдруг с какого-то момента добавляем в описание ещё и состояния поля
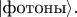
Применительно к электрону в атоме описание
схематично выглядит так (разумеется, всё в статистическом контексте, единственный экземпляр атома водорода во Вселенной в "Квантах" не может быть рассмотрен).
Пусть задано начальное (при
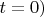
состояние системы "атом + поле":
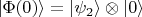
Здесь

это состояние атома в возбуждённом состоянии,

- состояние поля с числом фотонов, равным нулю. К моменту времени

состояние системы эволюционирует под действием оператора эволюции

(его явное выражение зависит от оператора Гамильтона атома, поля, и оператора взаимодействия

электрона с полем):
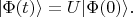
Получается:


это амплитуда вероятности обнаружить атом в невозбуждённом состоянии

и при этом поле в состоянии

с одним фотоном.

- амплитуда вероятности обнаружить систему всё ещё в начальном состоянии (т.е. атом возбуждён, фотонов нет). Вероятности равны квадратам модулей амплитуд вероятностей, их нормировка:
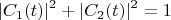
Если поле не заперто в резонаторе, то с ростом

вероятность
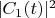
увеличивается, а
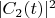
уменьшается. (Если же поле локализовано в резонаторе, то возможны квантовые биения, "осцилляции Раби". Для этого варианта тоже есть хорошо развитая теория и много интересных экспериментов, но далее этот вариант не обсуждаю.)
В расчёте амплитуд вероятности есть нюансы. Самый простой приближённый расчёт - в низшем порядке теории возмущений: разлагают

в ряд по степеням
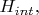
и вычисляют вклад первой степени в
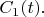
При этом волновые функции

и

берут "в нулевом порядке", т.е. как известные волновые функции электрона в атоме с известными энергиями

и

найденными из уравнения Шредингера со статическим потенциалом, без учёта квантованного электромагнитного поля.
Т.е. в этом приближении

и

это стационарные состояния со строго дискретными уровнями внутренней энергии атома

и

Как видно из выражения для
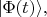
с течением времени они "запутываются" с состояниями фотонного поля; в целом получается суперпозиция нестационарных состояний системы. То же другими словами: получается суперпозиция стационарных состояний системы
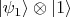
и
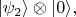
коэффициенты

и

которой зависят от времени (
это предложение я добавил позже, приношу извинения за такое медленное редактирование).
На языке экспериментатора речь идёт просто о том, что с течением времени увеличивается вероятность того, что возбуждённый атом
спонтанно излучит фотон. (Речь бы шла о
стимулированном излучении, если бы фотон излучался атомом под воздействии приходящего извне излучения, но в данной задаче нет внешнего излучения: начальное состояние фотонного поля задано как ноль фотонов, "фотонный вакуум".)
Оператор

в КЭД пропорционален
малому параметру

где
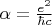
- так называемая "постоянная тонкой структуры", здесь

- заряд электрона,

- скорость света;
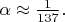
(
upd 18.09.2025: исправил это предложение; сначала я в спешке неправильно "вспомнил", что такое постоянное тонкой структуры. Важно, что  содержит в качестве сомножителя заряд электрона, и проявления взаимодействия электрона с фотонами в наблюдаемых вероятностях оказываются малыми вследствие малости
содержит в качестве сомножителя заряд электрона, и проявления взаимодействия электрона с фотонами в наблюдаемых вероятностях оказываются малыми вследствие малости 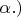
Поэтому величина
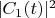
хотя и растёт с ростом

примерно пропорционально

но остаётся много меньшей единицы даже на достаточно больших временах
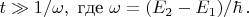
А ответ в теории возмущений и можно считать достаточно точным, только пока
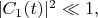
так как обратное неравенство будет бессмысленным (ведь правильно вычисленная вероятность не может быть больше единицы).
Таким образом вводится "скорость перехода"
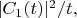
она же "вероятность перехода из состояния 2 в состояние 1 за единицу времени", она же обратное "время жизни"

состояния 2.
Другими словами, в этом приближении получается
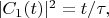
где

вычисляется по теории возмущений в КЭД.
Соответственно, вероятность
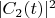
в этом же приближении равна
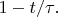
Это можно понимать как низшие члены разложения по степеням

а более точная формула для вероятности возбуждённого состояния есть

В свою очередь это означает, что с учётом взаимодействия с квантованным электромагнитным полем возбуждённое состояние атома не имеет вида строго стационарного состояния, а может описываться как квазистационарное состояние - с мнимой добавкой к энергии. Т.е. вместо
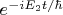
зависящая от времени волновая функция возбуждённого состояния содержит такого же вида сомножитель, но с энергией
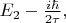
и для вероятности получается как раз
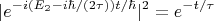
Величину
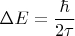
называют шириной уровня энергии квазистационарного состояния, а само соотношение вида

называют соотношением неопределённости для энергии.
Малостью постоянной тонкой структуры обеспечивается малость ширины энергетических уровней у атомов по сравнению с разностями энергий уровней
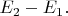
Это счастливое обстоятельство и привело в истории физики к открытию дискретных оптических спектров атомов, затем к идее Бора о дискретности внутренней энергии атома и о связи межуровневых интервалов с энергией фотона
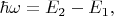
затем к КМ и КЭД.
В КЭД ширины уровней вычисляются, и они оказываются в согласии с наблюдениями в опытах, где ширины уровней

проявляются как ширины
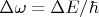
линий оптических спектров. (Точнее говоря, в опытах всё несколько сложнее, так как есть ещё и другие причины уширения спектральных линий, например, - доплеровское уширение из-за движения атомов. Полный энергетический спектр атома с учётом движения центра масс непрерывен; дискретным можно считать (причём только приближённо, если учитывается КЭД) спектр внутренней энергии атома.)
Такого рода темы из квантовой физики - довольно интересные; и нужные в образовательном плане. Хорошо бы для них создавать отдельные ветки. А философия "теории измерений", "ММИ и прочих интерпретаций КМ" это сбоку бантик. ИМХО, ес-нно. Как-то не хочется всерьёз разбирать физику в ветке, предназначенной для "пофилософствовать в перекурах".