Грубые нарушения элементарной логики

[BorisK]

EminentVictorians в сообщении #1701967 писал(а):

С учетом того, что мы только что выяснили, что отношение $R \subset D^n$, как вы объясните эту фразу:

Цитата:

Изменение 2. Для многих задач логического анализа удобно рассматривать n-местное отношение не как множество n-местных кортежей элементов, а как объединение ДП.

(ДП - это у вас аббревиатура для декартова произведения). Объединение каких ДП?

Это как бы преамбула. Далее все более строго определяется через атрибуты, схемы отношения и т.д. А здесь вот что имеется в виду. Некоторые отношения можно выразить как ДП, например, $R_1=A \times B$. Возможны другие подобные отношения, например, $R_2=B \times C$. И допустимы такие отношения как $R_3= R_1 \cup R_2$. По сути, сжатая форма традиционного отношения. А кортеж элементов тоже можно представить как частный случай ДП: $\{a\} \times \{b\}$.

[EminentVictorians]

BorisK в сообщении #1701987 писал(а):

Это как бы преамбула. Далее все более строго определяется через атрибуты, схемы отношения и т.д. А здесь вот что имеется в виду. Некоторые отношения можно выразить как ДП, например, $R_1=A \times B$. Возможны другие подобные отношения, например, $R_2=B \times C$. И допустимы такие отношения как $R_3= R_1 \cup R_2$. По сути, сжатая форма традиционного отношения. А кортеж элементов тоже можно представить как частный случай ДП: $\{a\} \times \{b\}$.

Так у вас уже полно ошибок... Нельзя объекты произвольно по своему желанию называть отношениями. Вообще, в математике нет такого термина как просто "отношение". Это бессмысленный набор букв. Осмысленно, например, словосочетание "бинарное отношение R, заданное на множествах $A$ и $B$". Поэтому, если отношение $R_1$ - это корректно определенное универсальное отношение на множествах $A$ и $B$, отношение $R_2$ - тоже корректное универсальное отношение, то $R_3$ - это никакое не отношение, а просто объединение двух множеств.

BorisK в сообщении #1701987 писал(а):

А кортеж элементов тоже можно представить как частный случай ДП: $\{a\} \times \{b\}$.

Нет. Кортеж $(a, b)$ элементов $a$ и $b$ - это элемент множества $\{a\} \times \{b\}$. Вообще, в таких темах очень не желательно использовать все эти неформальные словосочетания типа "представить", "выразить" и т.д. - надо конкретно говорить, кто кому принадлежит.

-- 15.09.2025, 19:02 --

Кстати, для вас это может быть хорошим упражнением. Попробуйте дать корректную формулировку, в которой $R_3$ действительно будет корректно определенным отношением.

[Mikhail_K]

EminentVictorians в сообщении #1701992 писал(а):

BorisK в сообщении #1701987 писал(а):

Это как бы преамбула. Далее все более строго определяется через атрибуты, схемы отношения и т.д. А здесь вот что имеется в виду. Некоторые отношения можно выразить как ДП, например, $R_1=A \times B$. Возможны другие подобные отношения, например, $R_2=B \times C$. И допустимы такие отношения как $R_3= R_1 \cup R_2$. По сути, сжатая форма традиционного отношения. А кортеж элементов тоже можно представить как частный случай ДП: $\{a\} \times \{b\}$.

Так у вас уже полно ошибок... Нельзя объекты произвольно по своему желанию называть отношениями. Вообще, в математике нет такого термина как просто "отношение". Это бессмысленный набор букв. Осмысленно, например, словосочетание "бинарное отношение R, заданное на множествах $A$ и $B$". Поэтому, если отношение $R_1$ - это корректно определенное универсальное отношение на множествах $A$ и $B$, отношение $R_2$ - тоже корректное универсальное отношение, то $R_3$ - это никакое не отношение, а просто объединение двух множеств.

Как я понял, он рассматривает все множества $A$, $B$, $C$, $\ldots$ как подмножества некоторого множества $D$ (или $X$?) Тогда и $R_1=A\times B$, и $R_2=B\times C$, и их объединение будут бинарными отношениями на этом универсальном множестве.

Вообще, у меня впечатление после беглого знакомства с творчеством BorisK, что явных грубых ошибок у него нет, но много банальностей, неточностей и своей авторской терминологии, иногда нечётко определённой. И даже когда он отрицает равномощность счётных множеств, на самом деле он готов согласиться с тем, что равномощность в принятом в математике смысле там может и есть, просто он сам хочет равномощность определять по-другому, а может быть, и вообще обойтись без этого понятия. Научной ценности в этих (псевдо)математических построениях не видно, но и явных ошибок вроде бы тоже. Хотя, может быть, если поискать, то они найдутся.

[EminentVictorians]

Mikhail_K в сообщении #1702003 писал(а):

Как я понял, он рассматривает все множества $A$, $B$, $C$, $\ldots$ как подмножества некоторого множества $D$ (или $X$?)

Не совсем так. Он их рассматривает как подмножества соответственно $X_1, X_2,X_3$ (или $D_1, D_2, D_3$ - я так и не понял, зачем вводить обозначение с иксами, если область интерпретации он обозначает буквой D).

Mikhail_K в сообщении #1702003 писал(а):

Вообще, у меня впечатление после беглого знакомства с творчеством BorisK, что явных грубых ошибок у него нет, но много банальностей, неточностей и своей авторской терминологии, иногда нечётко определённой.

Ну не знаю, у меня другое впечатление. Я во всей его статье не нашел ни одного корректного определения.

[BorisK]

EminentVictorians в сообщении #1702005 писал(а):

Я во всей его статье не нашел ни одного корректного определения.

EminentVictorians в сообщении #1701992 писал(а):

Кстати, для вас это может быть хорошим упражнением. Попробуйте дать корректную формулировку, в которой $R_3$ действительно будет корректно определенным отношением.

В научном творчестве иногда случается так, что некто придумывает какую-то штуковину, а затем кому-то приходится уточнять терминологию, входящую в нее. У меня, как это ни смешно, процесс уточнения терминологии затянулся на 30 с лишним лет и до сих пор продолжается. Так что, если хотите мне помочь, то лучше будет не копаться в опубликованной статье, а проверить на предмет ошибок небольшую составленную мною недавно систему определений. Согласны? И на каких условиях?
Наверное, юмор в том, что я по натуре гуманитарий с техническим образованием (горный инженер). Даже в 1997 и 2001 гг. написал пару философских книг по научному творчеству, за которые меня, по-видимому, ненавидят некоторые мои влиятельные коллеги из сферы искусственного интеллекта и логики. Но, вот решил почему-то заняться математикой.

[EminentVictorians]

BorisK в сообщении #1702028 писал(а):

Так что, если хотите мне помочь, то лучше будет не копаться в опубликованной статье, а проверить на предмет ошибок небольшую составленную мною недавно систему определений. Согласны?

Так вы её выкладывайте сюда на форум, эту систему определений. Тем более, если она небольшая.

[BorisK]

EminentVictorians в сообщении #1702030 писал(а):

Так вы её выкладывайте сюда на форум, эту систему определений. Тем более, если она небольшая.

А если исправленная система войдет в статью или в книгу, то кого я могу поблагодарить?

[EminentVictorians]

BorisK, выкладывайте уже.

[BorisK]

EminentVictorians в сообщении #1702032 писал(а):

BorisK, выкладывайте уже.

Во второй половине дня выложу.

[Mihr]

BorisK в сообщении #1702031 писал(а):

А если исправленная система войдет в статью или в книгу, то кого я могу поблагодарить?

Форум.

(Оффтоп)

Ваш КО. Не благодарите

[Geen]

(Оффтоп)

Mihr в сообщении #1702037 писал(а):

Форум

А нам нужна такая реклама?

[mihaild]

(Оффтоп)

Geen в сообщении #1702038 писал(а):

А нам нужна такая реклама?

Там же потом уточнение.

Mihr в сообщении #1702037 писал(а):

Не благодарите

[BorisK]

А что означает КО?

[Sender]

BorisK в сообщении #1702040 писал(а):

А что означает КО?

https://ru.wikipedia.org/wiki/Капитан_Очевидность

[BorisK]

Предлагаю для критики систему определений.

Используемые сокращения:
АК – алгебра кортежей;
ДП – декартово произведение множеств;
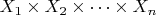
Далее под отношением подразумевается $n$-местное отношение, определяемое как подмножество ДП ${X_1 \times X_2 \times \dots \times X_n}$, где $X_i$ - множества.

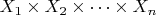
Пусть отношение $R$ задано как подмножество ДП ${X_1 \times X_2 \times \dots \times X_n}$. Будем считать данное ДП универсумом $\mathbf{U}$ этого отношения. Тогда $R \subseteq \mathbf{U}$.
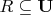
В дальнейшем будем называть имена множеств, из которых сформирован универсум, атрибутами этого отношения, элементы этих множеств – значениями соответствующих атрибутов, а сами множества значений – доменами этих атрибутов.

Элементарный кортеж – это кортеж элементов из разных доменов атрибутов, например, $(a,d,f)$.

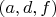
Схемой отношения называется заключенная в квадратные скобки последовательность атрибутов, ДП которых определено как универсум данного отношения.
Например, имя трехместного отношения $R_2[X_1X_4X_6]$ означает, что универсумом отношения $R_2$ является ДП ${\mathbf{U} = X_1 \times X_4 \times X_6}$.

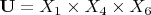
Однотипные отношения - отношения, заданные в одном и том же универсуме.

Компонентой называется произвольное подмножество домена атрибута.

Фиктивные компоненты:
- полная ($\ast$) равна домену соответствующего атрибута;
- пустая ($\emptyset$) равна пустому множеству.
Фиктивными они названы потому, что при добавлении к определенным структурам АК столбцов с фиктивными компонентами смысл отношения остается неизменным, но при этом появляется возможность выполнять операции и проверки равенства или включения для структур, имеющих разные схемы отношений.

АК-объекты - это варианты отображения отношений, которые являются сжатыми множествами однотипных $n$-местных элементарных кортежей. В АК определено четыре основных типа АК-объектов: $C$-кортежи (интерпретация конъюнкции одноместных предикатов с разными переменными), $C$-системы (интерпретация ДНФ), $D$-кортежи (интерпретация дизъюнкции одноместных предикатов с разными переменными) и $D$-системы (интерпретация КНФ).

$C$-кортеж - это отношение, равное ДП содержащихся в нем компонент, записанных в виде кортежа, ограниченного квадратными скобками.
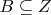
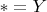
Например, АК-объект $T[XYZ] = \bigl[A~~\ast~~B \bigr]$ - это $C$-кортеж, при этом $A\subseteq X$, $B \subseteq Z$, а компонента $\ast$ равна домену соответствующего атрибута (в данном случае, поскольку она находится на второй позиции, то $\ast = Y$). Этот $C$-кортеж можно преобразовать в обычное отношение с помощью ДП следующим образом:
$T[XYZ] = A \times Y \times B$.

$C$-система - это отношение, равное объединению однотипных $C$-кортежей, которые записываются в виде строк матрицы, ограниченной квадратными скобками.
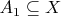
Например, $R[XYZ]=\left [\begin{array} {ccc} A_1 & \ast & A_3\\ B_1 & B_2 & \ast \end{array}\right]$ есть $C$-система, при этом $A_1 \subseteq X$, $A_3 \subseteq Z$ и т.д. Данная $C$-система преобразуется в обычное отношение с помощью ДП следующим образом:
$R[XYZ] = (A_1 \times Y \times A_3) \cup (B_1 \times B_2 \times Z)$.

С помощью $C$-кортежей и $C$-систем можно выразить любое многоместное отношение, но для вычисления их дополнений требуются новые структуры - $D$-кортежи и $D$-системы. Для определения этих АК-объектов используется промежуточная структура - диагональная $C$-система

Диагональная $C$-система - это $C$-система размерности $n \times n$, у которой все компоненты полные $(\ast)$ за исключением диагональных компонент.
Например, $Q[XYZ]= \left [\begin{array} {ccc} A & \ast & \ast\\ \ast & B & \ast\\ \ast & \ast & C \end{array}\right]$ - диагональная $C$-система.
Доказано, что диагональная $C$-система есть результат вычисления дополнения некоторого $C$-кортежа.

$D$-кортеж - это отношение, равное диагональной $C$-системе, записанное как ограниченный перевернутыми квадратными скобками кортеж ее диагональных компонент.
Например, изображенную выше диагональную $C$-систему можно записать как $D$-кортеж:
$Q[XYZ] = \bigl] A~~B~~C \bigr[$.

$D$-система - это отношение, равное пересечению однотипных $D$-кортежей, записанное как ограниченная перевернутыми квадратными скобками матрица компонент, в которой строками являются участвующие в операции $D$-кортежи.