В Вашей статье на стр. 13 этого тоже нет. Я вижу там только произвольно определённое понятие "конечной фиксации ряда". Но с какое стати Вы определяете "конечную фиксацию ряда" именно так?
Не настаиваю на том, что в статье дано точное определение. Но разве нельзя бесконечный ряд
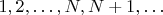
определить по индукции? И определить количество

четных чисел в этом ряде как функцию от

, принимающую 2 возможных значения в зависимости от того, четное

или нечетное, и доказать, что при стремлении

к бесконечности отношение
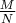
при обоих значениях функции стремится к 0,5?
Но если мы посчитаем отношение количества чётных к количеству всех чисел для каждого конечного множества - элемента последовательности, то предел такого отношения будет равен

.
В Вашей последовательности не соблюдается естественное правило: в ней должны присутствовать все целые положительные числа, не превосходящие числа

. А иначе можно строить последовательности с любыми мерами отношений в пределах от 0 до 1 для четных чисел .
Математика с бесконечностями ("актуальными", как Вы говорите), конечно, в чём-то парадоксальнее, зато гораздо удобнее, чем математика без бесконечностей.
Удобство понятие растяжимое. А парадоксальность, насколько мне известно, не всех авторитетных математиков удовлетворяла. Я не отрицаю бесконечности. Но разве не возможна (хотя бы в некоторой своей части) математика с потенциальной бесконечностью? И разве методами обычной математической (потенциальной) индукции не доказаны многие основополагающие результаты функционального анализа?
Не знаю, что Вы хотели этим примером показать, но "задача" решается в уме за два перекура.
Вот здорово! Не опишете ли, хотя бы схематично, как Вы ее решили, и какие методы использовали?
Но главный вопрос остаётся: где здесь какие-то "ранее неизвестные свойства" декартового произведения?
Я уже устал перечислять. Может быть, слово «свойство» здесь не подходит? Речь идет о неизвестных ранее операциях, проверках включения и интерпретации объединений декартовых произведений. И потом это всего лишь Ваше мнение об отсутствии новизны, которое было бы более убедительным, если бы Вы его обосновали. И все равно оно, скорее всего, так и останется мнением, поскольку существуют в некоторых случаях документально подтвержденные альтернативные мнения.
Меня здесь интересует вот эта фраза:
Цитата:
...является n-местное отношение, т.е. подмножество n-местных кортежей элементов из

.
n-местное отношение, о котором идет речь - это отношение на каком множестве? Было бы совсем замечательно, если бы вы написали это формулой. Допустим

- то самое n-местное отношение. Тогда
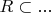
? Продолжите эту запись, чтобы было понятно, на каком множестве задано это отношение.

в данном случае это декартово произведение, т.е. множество

-местных кортежей, содержащих элементы из

. Чтобы продолжить запись
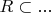
требуются некоторые пояснения. Отношения в АК определены вместе со схемой отношения, например,
![$R[X_1X_2X_5]$ $R[X_1X_2X_5]$](https://dxdy-02.korotkov.co.uk/f/d/4/8/d487d2eb60d85daf0ed96f36b711647982.png)
, где

- идентификаторы некоторых множеств. Тогда
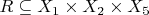
. В статье моя небрежность в том, что я не сказал, что

это декартово произведение. Но в цитируемом источнике это есть. И еще в моей статье сказано, что

это множество. Тогда запись

вряд ли может быть чем-то иным, чем декартово произведение.
Ой, у меня неотложных дел накопилась куча. Так что я беру отгул на недельку и прошу извинить меня тех участников дискуссии, на замечания и вопросы которых я в ближайшее время не смогу ответить.