«Для справки: в АК 30 с лишним теорем описывают свойства ДП и только 3 теоремы из них – те свойства, которые были известны до АК». Например?
Более точно речь идет о теоретико-множественных операциях и соотношениях для ДП. Чтобы мой ответ был более понятен, должен сказать, что в АК введены
схемы отношений для АК-объектов. Если состав атрибутов в схемах отношения АК-объектов совпадает, то они
однотипные. До АК были известны следующие 3 свойства: 1) алгоритм проверки включения однотипных ДП; 2) алгоритм вычисления пересечения двух однотипных ДП; 3) алгоритм вычисления разности двух однотипных ДП. В АК введены операции объединения и дополнения для ДП и их объединений. Причем возможны операции и проверки включения не только для однотипных АК-объектов, но и для случаев, когда у них разные схемы отношения. Осуществляется это с помощью операции добавления фиктивного атрибута, которая соответствует правилу обобщения для языка первого порядка по версии, которая изложена в разных изданиях книги Э. Мендельсона.
и даже в английской Wikipedia
Приведите, пожалуйста, точную цитату, где упоминается "алгебра кортежей" и свойства, открытые с её помощью.
Приведу небольшие отрывки из большого раздела.
12 – ссылка на книгу Kulik, B. Fridman, A. (2022). Complicated Methods of Logical Analysis Based on Simple Mathematics. Cambridge Scholars Publishing.
Let us denote the Cartesian product as a tuple bounded by square brackets; this tuple includes the sets from which the Cartesian product is formed, e.g.:
![$A = A_1 \times A_2 \times \dots \times A_n =[A_1\quad A_2\quad \dots \quad A_n] $ $A = A_1 \times A_2 \times \dots \times A_n =[A_1\quad A_2\quad \dots \quad A_n] $](https://dxdy-02.korotkov.co.uk/f/5/4/2/5422ae8fcf9d0f9472ed97360da8c13282.png)
.
In
n-tuple algebra (NTA
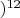
, such a matrix-like representation of Cartesian products is called a

-tuple.

Let us consider some new relations for structures with Cartesian products obtained in the process of studying the properties of NT
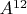
. The structures defined in the same universe are called
homotypic ones.
#
The intersection of C-systems. Assume the homotypic

-systems are given

and

. Their intersection will yield a

-system containing all non-empty intersections of each

-tuple from

with each

-tuple from

.
#
Checking the inclusion of a C-n-tuple into a D-n-tuple. For the

-tuple
![$P = [P_1 \quad P_2 \quad \cdots \quad P_N]$ $P = [P_1 \quad P_2 \quad \cdots \quad P_N]$](https://dxdy-04.korotkov.co.uk/f/b/9/c/b9c29369ca3eb807b130388f94ce8a8782.png)
and the

-tuple
![$Q = ]Q_1 \quad Q_2 \quad \cdots \quad Q_N[$ $Q = ]Q_1 \quad Q_2 \quad \cdots \quad Q_N[$](https://dxdy-02.korotkov.co.uk/f/d/8/b/d8b30f4b605a11977974045b1f548ffc82.png)
holds
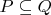
, if and only if, at least for one

holds
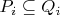
.
#
Checking the inclusion of a C-n-tuple into a D-system. For the

-tuple

and the

-system

is true
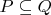
, if and only if, for every

-tuple
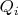
from

holds
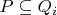
.