Философский оффтоп из темы Интерпретации квантовой механики

[EminentVictorians]

epros в сообщении #1699605 писал(а):

Авторы силлогистики, типа Аристотеля или Боэция, кванторов не знали. Но они отличали "общие" утверждения от "частных" (см. логический квадрат).

Все равно не понимаю. У них тексты пестрят словами "каждый" и "некоторый". Чем не кванторы?

[Anton_Peplov]

EminentVictorians в сообщении #1699607 писал(а):

Все равно не понимаю. У них тексты пестрят словами "каждый" и "некоторый". Чем не кванторы?

Слова "каждый" и "некоторый" были известны задолго до античных логиков. Аристотель сформулировал некоторые правила обращения с ними, но не дошел до того компактного свода правил, который сейчас включен в аксиоматику логики предикатов первого порядка. Можно сказать, что Аристотель знал кванторы, но еще не вполне умел с ними работать.

[EminentVictorians]

Anton_Peplov в сообщении #1699609 писал(а):

Аристотель сформулировал некоторые правила обращения с ними, но не дошел до того компактного свода правил, который сейчас включен в аксиоматику логики предикатов первого порядка. Можно сказать, что Аристотель знал кванторы, но еще не вполне умел с ними работать.

Можно пример? Я единственное с чем готов согласиться, что у древних были какие-то проблемы с пустым множеством (высказываниями с пустым носителем). Но в остальном, мне сложно поверить, что есть пример какого-то рассуждения, которое в логике первого порядка имеется, а древние бы о нем не знали.

[epros]

EminentVictorians в сообщении #1699607 писал(а):

Все равно не понимаю. У них тексты пестрят словами "каждый" и "некоторый". Чем не кванторы?

С квантором связаны конкретные правила применения: с ним должна быть связана переменная, она может быть в определённых позициях в формуле под квантором, она не должна быть закрыта тем квантором, который уже был в той формуле, которая под квантором. Кроме того, есть определённые синтаксические правила подстановки термов вместо переменных, связанных с кванторами. А ещё есть аксиоматика, определяющая кванторы. Ничего этого в силлогистике не было.

-- Пн авг 25, 2025 14:36:48 --

EminentVictorians в сообщении #1699611 писал(а):

есть пример какого-то рассуждения, которое в логике первого порядка имеется, а древние бы о нем не знали.

Что значит "древние бы не знали"? Формулу первого порядка можно изложить словами естественного языка, каждое из которых и общую грамматику построения предложения древние наверняка знали. Но иногда может получиться настолько сложно, что при рассуждениях с такими предложениями древние наверняка бы запутались.

[EminentVictorians]

epros в сообщении #1699612 писал(а):

с ним должна быть связана переменная

Ну вот тот самый силлогизм про Сократа: для любого человека известно, что человек смертен. Человек здесь и есть та переменная, которую "связывает" квантор всеобщности и вместо которой подставляются имена конкретных людей.

epros в сообщении #1699612 писал(а):

она не должна быть закрыта тем квантором, который уже был в той формуле, которая под квантором.

"Какую лошадь ни возьми, она рано или поздно устанет". "Какую ни возьми" - это квантор всеобщности на переменную лошадь. "Рано или поздно устанет" - это значит, что существует временной период эксплуатации лошади, при котором она потеряет значительную часть своих сил. Здесь квантор существования находится внутри "формулы" на которую снаружи навешан квантор всеобщности. Думаете древние не поняли бы, какой квантор к чему тут относится?

epros в сообщении #1699612 писал(а):

Что значит "древние бы не знали"? Формулу первого порядка можно изложить словами естественного языка, каждое из которых и общую грамматику построения предложения древние наверняка знали. Но иногда может получиться настолько сложно, что при рассуждениях с такими предложениями древние наверняка бы запутались.

Но тезис то в том, что они какие-то правила оперирования с кванторами вообще не знали. Вот мне и хочется узнать, какие конкретно.

[epros]

EminentVictorians в сообщении #1699618 писал(а):

Ну вот тот самый силлогизм про Сократа: для любого человека известно, что человек смертен. Человек здесь и есть та переменная, которую "связывает" квантор всеобщности и вместо которой подставляются имена конкретных людей.

Не совсем. "Человек" и "смертный" - это свойства объектов, а квантор всеобщности стоит на переменной, обозначающей любой объект.

EminentVictorians в сообщении #1699618 писал(а):

"Какую лошадь ни возьми, она рано или поздно устанет". "Какую ни возьми" - это квантор всеобщности на переменную лошадь. "Рано или поздно устанет" - это значит, что существует временной период эксплуатации лошади, при котором она потеряет значительную часть своих сил. Здесь квантор существования находится внутри "формулы" на которую снаружи навешан квантор всеобщности. Думаете древние не поняли бы, какой квантор к чему тут относится?

Это не о том. У Вас квантор существования стоит на другой переменной, обозначающей промежуток времени. А синтаксическое правило о том, что если вдруг под внешним и внутренним кванторами одна и та же переменная, то к внутренней формуле внешний квантор не относится. Здесь надо ещё исхитриться понять, в каком смысле лошадей и промежутки времени можно обозначить одной переменной. Во всяком случае, в бинарный предикат "устанет", имеющий в качестве первого аргумента лошадь, а в качестве второго - промежуток времени, очень странно подставлять одну и ту же переменную в оба его аргумента.

EminentVictorians в сообщении #1699618 писал(а):

Но тезис то в том, что они какие-то правила оперирования с кванторами вообще не знали. Вот мне и хочется узнать, какие конкретно.

Ну, я даже не знаю, что сказать. Вот есть правило объединения импликаций по антецеденту, означающее, что если $\psi$ не имеет свободных вхождений переменной $x$, то формула $\forall x~(\varphi \to \psi)$ приводится к формуле $(\exists x~\varphi) \to \psi$. Знали древние это правило или нет?

[pppppppo_98]

realeugene в сообщении #1699597 писал(а):

А на каком языке написана книга?

Мне почему то кажется что скачать бы заняло меньше времени,чем спросить... На стандартном для такого рода литературы - на английском. Если вас интересуют нестандартные логики может быть проще залезть на какую нибудь энциклопедию Аля Вика, ncatlab, mathplanrt, stackproject ... Тама час то и густо много чо выкладывают и по топосам(одна из нестандартных логик), и по теории множеств, категорий и прочий связанный матаппарат.

[EminentVictorians]

epros в сообщении #1699621 писал(а):

квантор всеобщности стоит на переменной, обозначающей любой объект.

А по мне, квантор стоит на переменной "человек", пробегающей значения из множества всех людей. Мне гораздо проще воспринимать формулы вида ($\forall x \in M$) $P(x)$, а не ($\forall x$) $(x \in M \to P(x))$.

epros в сообщении #1699621 писал(а):

А синтаксическое правило о том, что если вдруг под внешним и внутренним кванторами одна и та же переменная, то к внутренней формуле внешний квантор не относится.

Так это банальность. Это как в математике писать что-то типа:

$$f(x) = x^{\lim\limits_{x \to 3}^{}x^2$$

или

$$f(x) = \int\limits_{a}^{x} g(x)dx$$

Можно, но зачем? Гораздо разумнее переименовать переменную и все:

$$f(x) = x^{\lim\limits_{t \to 3}^{}t^2$$

$$f(x) = \int\limits_{a}^{x} g(t)dt$$

Древние такие вещи на раз бы выкупили. Да, у них не было символьного языка, но они вполне понимали и что такое предикат, и что такое свободная и связанная переменная. Для этого формальная логика не нужна.

epros в сообщении #1699621 писал(а):

Ну, я даже не знаю, что сказать. Вот есть правило объединения импликаций по антецеденту, означающее, что если $\psi$ не имеет свободных вхождений переменной $x$, то формула $\forall x~(\varphi \to \psi)$ приводится к формуле $(\exists x~\varphi) \to \psi$. Знали древние это правило или нет?

Ну т.е. если перевести это все на обычный человеческий язык, то получится примерно так: есть какое-то множество, пусть $M = \{1, 2, 3\}$. Переменная $x$ пробегает множество $M$. Есть так же предикат $\varphi(x)$ зависящий от $x$. Мы каким-то образом умудрились доказать, что какой-бы $x$ ни был, если при нем $\varphi(x)$ вдруг окажется истинным, то значит и $\psi$ тоже будет истинным. То есть другими словами:

1) из истинности $\varphi(1)$ вытекает $\psi$
2) из истинности $\varphi(2)$ вытекает $\psi$
3) из истинности $\varphi(3)$ вытекает $\psi$

Можем ли мы утверждать теперь, что $\psi$ истинно? Разумеется, нет. Мы же не установили истинность ни одного из $\varphi(1)$, $\varphi(2)$, $\varphi(3)$. Но далее мы каким-то другим чудесным образом вдруг выяснили, что кто-то из них точно должен быть истинным (а может быть даже конкретно нашли, что истинным будет, допустим, $\varphi(2)$). Ну ясно дело, что значит и $\psi$ теперь будет истинно.

Вы серьезно думаете, что древние не поняли бы, о чем тут речь?

[realeugene]

pppppppo_98 в сообщении #1699623 писал(а):

Мне почему то кажется что скачать бы заняло меньше времени,чем спросить... На стандартном для такого рода литературы - на английском. Если вас интересуют нестандартные логики может быть проще залезть на какую нибудь энциклопедию Аля Вика, ncatlab, mathplanrt, stackproject ... Тама час то и густо много чо выкладывают и по топосам(одна из нестандартных логик), и по теории множеств, категорий и прочий связанный матаппарат.

переформулирую вопрос. А, случайно, не на языке ли обычной логики написана теория топосов?

-- 25.08.2025, 16:57 --

Anton_Peplov в сообщении #1699609 писал(а):

Можно сказать, что Аристотель знал кванторы, но еще не вполне умел с ними работать.

То есть можно сказать, что и Аристотель не изобретал логику, а открывал логику в естественном языке.

-- 25.08.2025, 16:59 --

epros в сообщении #1699605 писал(а):

Продвинутый язык развивается из не столь продвинутого. Договариваемся одновременно с закладыванием в язык того, о чём договариваемся.

А зачем, если не для описания окружающей реальности?

-- 25.08.2025, 17:00 --

epros в сообщении #1699605 писал(а):

и чувства у всех могут быть вполне одними и теми же.

Могут быть. На стадионе передаваемые невербально. А вот вербально чувства от одного к другому человеку не передаются, но могут быть инициированы в человеке.

-- 25.08.2025, 17:02 --

epros в сообщении #1699605 писал(а):

логика лежит глубже - в самом понимании того, что есть объекты и есть возможность называть их общим словом.

Ага, логика лежит в самом устройстве классического мира.

[epros]

EminentVictorians в сообщении #1699627 писал(а):

Мне гораздо проще воспринимать формулы вида ($\forall x \in M$) $P(x)$, а не ($\forall x$) $(x \in M \to P(x))$.

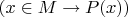
Первое - это просто жаргонная запись для второго, в то время как второе (в отличие от первого) формально соответствует синтаксису логики первого порядка, независимо от существования теории множеств и всяких там интерпретаций.

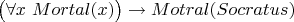
Можно, конечно, считать множество человеков за универсум и вообще их не упоминать. Но тогда меньшая посылка (Сократ - человек) вообще не нужна, а большая посылка будет звучать как: "Всё смертно". На языке исчисления предикатов: $\bigl(\forall x~Mortal(x)\bigr) \to Motral(Socratus)$ - банальная конкретизация всеобщности.

EminentVictorians в сообщении #1699627 писал(а):

Можно, но зачем? Гораздо разумнее переименовать переменную и все

Конечно разумнее. Но это просто синтаксис. Раз он такое позволяет, значит нужно понимать, как с этим работать.

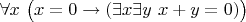
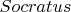
Например, вот синтаксически корректная формула: $\forall x~\bigl(x=0 \to (\exists x \exists y~x+y=0)\bigr)$, нужно просто понимать, что квантор всеобщности не относится к выражению $x+y=0$. Иначе можно ошибиться, например, при конкретизации всеобщности, скажем, подставить $Socratus$ вместо $x$ не только в $x=0$, но и в $x+y=0$.

EminentVictorians в сообщении #1699627 писал(а):

Да, у них не было символьного языка, но они вполне понимали и что такое предикат, и что такое свободная и связанная переменная.

По-моему, "предикаты" и "переменные" - это уже про символьный язык. А уж что они могли понимать под "связанной переменной" - это вообще интересный вопрос.

EminentVictorians в сообщении #1699627 писал(а):

Ну ясно дело, что значит и $\psi$ теперь будет истинно.

Вы серьезно думаете, что древние не поняли бы, о чем тут речь?

Откуда я знаю? Судя по тому, как они много веков косячили в своих силлогизмах с утверждениями о существовании, вполне могли не так понять. Понадобилось дожить до Бертрана Рассела с его примером про золотые горы (см. статью википедии про категорический силлогизм), чтобы понять, что это косяки.

-- Пн авг 25, 2025 18:45:51 --

realeugene в сообщении #1699629 писал(а):

А зачем, если не для описания окружающей реальности?

Для общения. Получаемые от собрата сообщения, конечно, тоже являются реальностью, но достаточно специфического вида.

realeugene в сообщении #1699629 писал(а):

А вот вербально чувства от одного к другому человеку не передаются, но могут быть инициированы в человеке.

Да ладно, сообщения о чувствах вполне могут быть понятны.

realeugene в сообщении #1699629 писал(а):

Ага, логика лежит в самом устройстве классического мира.

Это утверждение ни на чём не основано.

[pppppppo_98]

realeugene в сообщении #1699629 писал(а):

А, случайно, не на языке ли обычной логики написана теория топосов?

Случайно нет.

[EminentVictorians]

epros в сообщении #1699633 писал(а):

Но это просто синтаксис. Раз он такое позволяет, значит нужно понимать, как с этим работать.

Так это просто артефакт формальных систем. У древних не было формальных систем, но мне кажется все они прекрасно понимали, какая переменная связана каким квантором. Все эти вещи - кванторы, переменные, предикаты, свободные и связанные вхождения - имеют к формальным системам крайне косвенное отношение.

epros в сообщении #1699633 писал(а):

Судя по тому, как они много веков косячили в своих силлогизмах с утверждениями о существовании, вполне могли не так понять.

Да, я говорил про это парой сообщений выше (про высказывания с пустым носителем). Это единственное место у древних, которое они похоже не до конца понимали. И что забавно, формальная логика даже здесь не нужна.

[epros]

EminentVictorians в сообщении #1699640 писал(а):

мне кажется все они прекрасно понимали, какая переменная связана каким квантором

В каком смысле это можно было понимать, не имея ни кванторов (а только слова "все" и "некоторые" вместо них), ни переменных (в логике в целом, переменные в алгебре конечно были)?

EminentVictorians в сообщении #1699640 писал(а):

Это единственное место у древних, которое они похоже не до конца понимали. И что забавно, формальная логика даже здесь не нужна.

А что нужно? Я вот могу предположить, что если им сформулировать какое-нибудь $\forall x~(\varphi \to \psi)$ с не зависящей от квантора $\psi$, то они вполне бы могли бы прийти к выводу, что $\psi$ истинна без всяких предпосылок. Правда я не понимаю, как бы это всё звучало в языке силлогистики (может быть: "Все люди таковы, что Сократ смертен"?). Но с какой стати они должны были обязательно прийти к правильному выводу: что предпосылкой истинности $\psi$ является $\exists x~\varphi$? Ваше рассуждение тоже не совсем понятно. Вы просто перебрали все возможные $x$ и если нашли хотя бы одно истинное $\varphi(x)$, то сделали вывод об истинности $\psi$, а если не нашли, то не сделали. Но кто Вам сказал, что все $x$ вообще можно перебрать?

[EminentVictorians]

epros в сообщении #1699646 писал(а):

В каком смысле это можно было понимать, не имея ни кванторов (а только слова "все" и "некоторые" вместо них), ни переменных (в логике в целом, переменные в алгебре конечно были)?

Не имея формальных переменных. В том силлогизме про Сократа "человек" - это переменная, просто не формальная. Такие переменные у них были. У них не было формальных переменных. Формальная переменная отличается тем, что она должна быть частью формальной системы.

epros в сообщении #1699646 писал(а):

А что нужно?

Неформализованная логика. Та, которую я называю обычной человеческой логикой. Давайте докажем, что все марсиане любят пиво. Ну, предположим, что таки не все. Значит существует марсианин, который не любит пиво. Очевидно, такого нету. Значит наше предположение ложно, следовательно первоначальное утверждение истинно. Все что я использовал - обычную нормальную логику. Неформализованную. Я даже не знаю, что такое импликация, я не знаю, что там из лжи следует. Я вообще никаких этих формальных вещей не знаю. Но рассуждать про пустое множество объектов мне это не мешает.

epros в сообщении #1699646 писал(а):

Ваше рассуждение тоже не совсем понятно. Вы просто перебрали все возможные $x$ и если нашли хотя бы одно истинное $\varphi(x)$, то сделали вывод об истинности $\psi$, а если не нашли, то не сделали. Но кто Вам сказал, что все $x$ вообще можно перебрать?

Нет, я не перебирал. Я там аккуратно написал:

EminentVictorians в сообщении #1699627 писал(а):

Но далее мы каким-то другим чудесным образом вдруг выяснили, что кто-то из них точно должен быть истинным (а может быть даже конкретно нашли, что истинным будет, допустим, $\varphi(2)$).

[epros]

EminentVictorians в сообщении #1699648 писал(а):

В том силлогизме про Сократа "человек" - это переменная, просто не формальная.

Это очень кривая трактовка, хотя не скажу, что невозможная. Переменным в исчислении предикатов не нужны содержательные имена, они именуются исключительно для отличения их друг от друга. Можно просто $x_1,x_2,\ldots$ и далее по списку. А если Вы непременно хотите, чтобы переменными были человеки, то Ваш силлогизм запишется как $\bigl(\forall human~Mortal(human)\bigr) \to Mortal(Socratus)$. Меньшая посылка из силлогизма вообще исчезла, потому что утверждение о том, что константу $Socratus$ можно подставлять вместо переменной $human$ записывать незачем в силу синтаксической очевидности: любые константы всегда могут быть подставлены вместо любых переменных.

EminentVictorians в сообщении #1699648 писал(а):

Все что я использовал - обычную нормальную логику.

Откуда она взялась эта Ваша "обычная нормальная логика"? Чтобы обосновать, что Вы имеете право на следующий шаг рассуждения, Вы должны сослаться на какое-то ранее принятое правило. "Давайте предположим..." - а где у Вас было записано, что такое "предположения" и чем они могут заканчиваться? Это вообще-то называется "условным выводом" и его правила должны быть определены и понятны собеседнику. "Значит существует..., который..." - а по какому правилу Вы отрицание всеобщности свели к существованию отрицания, откуда оно взялось, это правило? С какой стати дикий человек доисторических веков, не изучавший логики в школе, должен понять этот Ваш ход? И далее: с какой стати Вы перешли к "очевидно такого нет"? Собеседник должен понимать на каких основаниях вообще можно отрицать существование. "Значит предположение ложно" - откуда это взято? Вы где-то объясняли собеседнику, что результатом условного вывода является импликация с гипотезой в предпосылке? Что утверждение и отрицание одного и того же - это "противоречие"? Наконец, что импликация с противоречием в следствии - это отрицание предпосылки импликации? "Следовательно первоначальное утверждение истинно" - когда Вы успели договориться с собеседником о том, что двойное отрицание снимается?

Так что это Ваше доказательство кажется Вам "обычным" и "нормальным" исключительно потому, что всем этим правилам где-то Вас в той или иной форме (возможно, неявно) научили.

EminentVictorians в сообщении #1699648 писал(а):

Я там аккуратно написал: EminentVictorians в сообщении #1699627

писал(а):
Но далее мы каким-то другим чудесным образом вдруг выяснили, что кто-то из них точно должен быть истинным (а может быть даже конкретно нашли, что истинным будет, допустим, $\varphi(2)$).

Что значит "чудесным образом"? Нельзя получить ответ на не заданный вопрос. Если Вы получили ответ об истинности предпосылки при каком-то конкретном значении $x$, это одно. А если Вы получили ответ в форме: "Предпосылка верна при некотором значении $x$, попробуйте сами угадать при каком", то что Вы будете делать? Поверите? Или будете проверять? Как?