его можно изложить в 3 строчки
1. Можно заметить, что уравнения вида

, где a, b, c - вещественные числа,

- нечетное число.
2. Разделяются на множители как
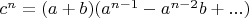
3. Откуда в следующей итерации мы имеем уравнение вида:
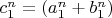
и получаем бесконечный спуск.
4. Существование целых чисел при этом невозможно.
5. Уравнение можно представить в виде
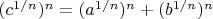
.
6. При любом нечетном значении n, и даже
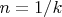
, где k - нечетное число, получаем решение

Ч.Т.Д.
Тут, конечно, все требует строго математического обоснования. Наверняка найдутся контрпримеры и т.п. А может и доказательство ошибочно...
Но не суть, значит найдется другое элементарное доказательство, которое также не будет иметь никакой математической ценности.
По крайней мере можно ответить на следующие вопросы:
1. Каким образом гипотеза стала теоремой еще задолго до своего доказательства?
2. Была ли надпись Ферма на полях книги оригинальной или кто-то ее дописал?
3. Почему ВТФ так притягивает ферматистов?
Допускаю, что во времена Ферма донести до аудитории суть вещественных чисел было настолько сложно, чем Ферма был вынужден заняться поиском решений в целых числах. А сама формулировка теоремы имеет двойной смысл - не имеет целочисленного решения и доказательства. Теорема состояла из теоремы и гипотезы. А Эндрю Уайлз, фактически, теорему Ферма не доказал, а опроверг гипотезу Ферма.
Формулировка из Википедии, на мой взгляд, не в полном объеме передает постановку задачи:
Теорема утверждает, что для любого натурального числа n > 2 уравнение вида

не имеет решений в целых ненулевых числах 
Я понял, что ничего не знаю, но многие не знают и этого...
Я те кто знает - молчит и смеется.
-- 16.08.2025, 17:55 --А в целом, если вас действительно интересует ВТФ, стоит почитать материалы форума. Узнаете много полезного.
Читал материалы форума. Ответа на свои вопросы не получил. Может читатели форума получат ответы на свои вопросы из моих постов.
Лучше что-то более разумное. Например Постников, "Великая теорема Ферма".
Полезный совет всем ферматистам. Только читайте внимательно, особенно стр.9.