1. Доказательство отсутствия нетривиальных целочисленных решений уравнения:

, где
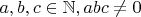
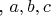
- взаимно-простые числа.
2. Введем параметр

, что:

3. Возводим обе части равенства п.2 в куб:
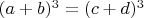
4. Из п.3 получаем:
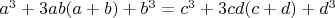
5. Упростим уравнение п.4:
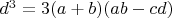
6. Из п.5 следует, что

делится на 3,
7. Пусть
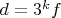
, где

не делится на 3.
8. Уравнение п.5 после замены с учетом п.7 примет вид:
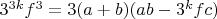
Рассмотрим 3 возможных случая:
Случай 1. 
делится на 3.
Найдем показатель степени при 3 для

. Для этого:
1.1. Равенство п.2 представим в виде:
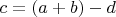
1.2. Возводим обе части уравнения п.1.1 в куб:
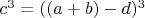
1.3. Раскрываем часть скобок уравнения п.1.2:
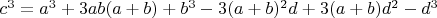
1.4. Подставляя исходные выражения и упрощая уравнение п.1.3, получаем:
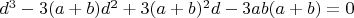
1.5. Сохранение условия делимости на 3 в уравнении п.1.4 возможно, если

делится на

, т.к.

делится на

.
1.6. Левая часть уравнения п.8 делится на

, правая – на

.
1.7. Из п.1.6 приравниваем показатели степеней при 3:
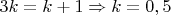
.
Но показатель степени при простом числе должен быть целым неотрицательным числом. Пришли к противоречию.
Случай 2. Ни одно из чисел

не делится на 3.
2.1. Из уравнения п.8 множитель
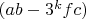
не делится на 3.
2.2. Приравниваем показатели степеней при 3 уравнения п.8:
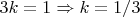
.
Получаем противоречие.
Случай 3. 
делится на 3.
3.1. Из уравнения п.8 получим:

делится на

Найдем показатель степени при 3 для

.
3.2. Исходное уравнение п.1 преобразуем к виду:
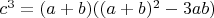
.
3.3. Из уравнения п.3.2 получим:

делится на

.
3.4. Проверим делимость на 3 левой и правой частей уравнения из п.2:

делится на

,
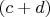
делится на

.
3.5. Приравнивая показатели степеней при 3 получим:
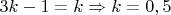
.
Пришли к противоречию.
ВЫВОД.Во всех рассмотренных случаях предположение о существовании нетривиальных целочисленных решений уравнения п.1 приводит к противоречиям в показателе степеней

при простом делителе 3.
Таким образом, уравнение не имеет нетривиальных решений в целых числах.
Ч.Т.Д.
-- 04.08.2025, 06:22 --P.S. В подтверждение правильности выбранного способа арифметического доказательства выполним следующий анализ:
4.1. Представим уравнение п.1 в следующем виде:
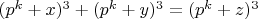
, где

- простое число.
4.2. Из уравнения п.4.1 получим:
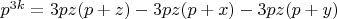
.
4.3. Из уравнения п.4.2:

. В общем виде ВТФ

.
Таким образом проверка делимости на

, в данном случае

, является ключом в решению ВТФ.
Аналогичным образом предположение о существовании нетривиальных целочисленных решений уравнений ВТФ при показателе степени

приводит к противоречиям в показателях степеней

при простом делителе

, кроме

.
Если я допустил критическую ошибку в доказательстве, значит я был неправ.