Какое число показать?

[mihaild]

EUgeneUS

(Оффтоп)

У меня получилась "показывать большее если $x^2 + y^2 < 1$ и большее иначе". Это вроде бы то же самое.

[wrest]

mihaild в сообщении #1693605 писал(а):

У меня получилась "показывать большее если $x^2 + y^2 < 1$ и большее иначе". Это вроде бы то же самое.

Я понял как "показывать большее если $x^2 + y^2 < 1$ и меньшее иначе"

Стратегия в pari

alice_strat_circle(x,y)=if(x^2+y^2<1,return([max(x,y),min(x,y)]),return([min(x,y),max(x,y)]));

Да, вроде все ранее предлагавшиеся тут стратегии Боба дают выигрыш ноль против этой стратегии Алисы.

[Shadow]

wrest в сообщении #1693611 писал(а):

Я понял как "показывать большее если $x^2 + y^2 < 1$ и меньшее иначе"

mihaild
Все точно. Проверено. Верно!

[worm2]

EUgeneUS в сообщении #1693602 писал(а):

Похоже, нашлась стратегия за Алису, причем чистая, которая обеспечивает ничью.

Делим квадрат $[0,1]^2$ на четыре области:
а) диагональю $y=x$
б) и четвертью окружности $y=\sqrt{1-x^2}$

В областях, которые граничат с горизонтальными сторонами квадрата, Алиса всегда показывает $x$
В областях, которые граничат с вертикальными сторонами квадрата, Алиса всегда показывает $y$

Браво!

Получается, верно тождество:

$$\int\limits_{x=0}^1\int\limits_{y=\sqrt{1-x^2}}^x \left[x(1-2g(y))+y(1-2g(x))\right]\,dx\,dy=\int\limits_{x=0}^1\int\limits_{y=0}^x x(1-2g(y))\,dx\,dy-\int\limits_{x=0}^1\int\limits_{y=x}^1 x(1-2g(y))\,dx\,dy$$

для любых функций $g: [0,1] \to [0,1]$.

Я не понимаю даже, как его доказать, не говоря уже о том, чтобы отыскать такую функцию, которая его обеспечивает. Для меня это какое-то волшебство!

[mihaild]

worm2 в сообщении #1693635 писал(а):

Я не понимаю даже, как его доказать

Поменяйте порядок интегрирование, чтобы перенести $g(y)$ во внешний интеграл.

Как найти - и правда непонятно. Я градиентным спуском оптимизировал стратегию Алисы (считая градиент через оптимальный ответ Боба), получил вот такую картинку (для вероятности назвать $y$)

Вложение:

download.png

И дальше угадал. Аналитически я дошел до уравнения (эквивалентного многим вариантам в теме) $\int_0^x p_{xy}y\, dy = \int_x^1 p_{xy}y\, dy$.

[EUgeneUS]

worm2
Спасибо!

worm2 в сообщении #1693635 писал(а):

Я не понимаю даже, как его доказать, не говоря уже о том, чтобы отыскать такую функцию, которая его обеспечивает.

Я тоже. Поэтому пришлось изобретать другой метод.

1. Ключевой момент - если равновесие Нэша существует, то при нём выигрыши сторон нулевые.
Не помню, возможно это доказанный результат для игр с двумя игроками и нулевым банком. Но в любом случае это устанавливается через Ваш функционал (или аналогичный), попутно выясняем стратегию Боба в равновесии Нэша.

2. Далее задаёмся вопросом: а какой ожидаемый выигрыш Боба, если он использует крайнюю стратегию и видит число $\xi$? Если ожидаемый выигрыш Боба ноль, то и смена стратегии ему не поможет.

Это приводит к функционалу:

$$W_2(\xi) = 2 \int\limits_{0}^{\xi} h(\xi, y) y dy - 2 \int\limits_{\xi}^{1} h(\xi, y) y dy + \xi^2 - \frac{1}{2}$$

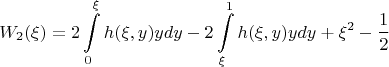
тут $h(x, y)$ - антисимметричная часть $f(x,y)$.

Если мы обеспечим ноль этого функционала для каждого $\xi$, то это и будет стратегия Алисы в равновесии Нэша. Точнее из найденного $h(x, y)$ восстановим $f(x,y)$, что и будет стратегией.

Как это решать в общем случая, не знаю. Но уважаемый mihaild всячески намекал, что есть чистая стратегия

-- 08.07.2025, 18:27 --

Чистая стратегия ищется так.
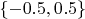
3. Сведем требования $h(x, y)$ в кучу. Окажется, что эта функция принимает значения $\{-0.5, 0.5\}$ на разных подмножествах квадрата.

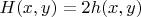
Для удобства перейдем к $H(x,y) = 2 h(x, y)$, она принимает значения $\{-1, 1\}$, при этом при переходе через $y=x$ знак обязан измениться (так как антисимметричная).

Функционал теперь:

$$W_2(\xi) = \int\limits_{0}^{\xi} H(\xi, y) y dy - \int\limits_{\xi}^{1} H(\xi, y) y dy + \xi^2 - \frac{1}{2}$$

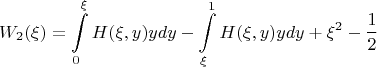
4. теперь пусть $\xi$ достаточно близко к $0$ и между $0$ и $\xi$ нет границ областей с разными значениями $H(x, y)$.
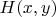
(не факт, что оно такое, но вдруг? )

Смотрим, что происходит с функционалом.
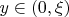
а) $y \in (0, \xi)$: выигрыш Боба $\int\limits_{0}^{\xi} y dy$
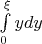
б) Далее при $H(x,y)$ обязано изменить знак, второй интеграл меняет знак и Боб опять выигрывает.
в) до $y=1$ так продолжаться не может, поэтому упрёмся в границу области, где опять $H(x,y)$ поменяет знак.
г) пусть граница области описывается функцией $y=g(x)$

Тогда функционал перепишется как (после перегруппировки интегралов)

$$W_2(\xi) = \int\limits_{0}^{g(\xi)} y dy - \int\limits_{g(\xi)}^{1} y dy + \xi^2 - \frac{1}{2}=0$$

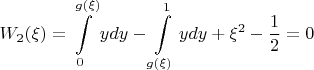
5. Собственно говоря, всё. Отсюда находится $g(x) = \sqrt{1-x^2}$
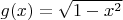
Нужно выполнить ещё несколько проверок, что всё хорошо. Но они проходят удачно.

[mihaild]

EUgeneUS в сообщении #1693640 писал(а):

Ключевой момент - если равновесие Нэша существует, то при нём выигрыши сторон нулевые.
Не помню, возможно это доказанный результат для игр с двумя игроками и нулевым банком. Но в любом случае это устанавливается через Ваш функционал (или аналогичный), попутно выясняем стратегию Боба в равновесии Нэша.

Это неправда. Например в игре "Алиса платит Бобу 1" цена игры ненулевая.
И в данном случае я не вижу причин априори считать, что цена игры нулевая. Но просто так получилось.

[wrest]

Я кстати не нашел на math.se ответа...
Задачу вроде нашел но в немного другой формулировке.

-- 08.07.2025, 18:41 --

worm2 в сообщении #1693635 писал(а):

Браво!

Присоединяюсь!

[mihaild]

wrest в сообщении #1693643 писал(а):

Я кстати не нашел на math.se ответа

https://math.stackexchange.com/a/5080568/659499
Возможно, вы нашли другую задачу (на которую есть ссылка в комментариях) - платит всегда Алиса, а Боб выбирает, взять показанное число или спрятанное.

[wrest]

mihaild в сообщении #1693644 писал(а):

Возможно, вы нашли другую

Да, потому что в задаче по ссылке нет Боба и Алисы, а есть Дилер и Игрок :)

[EUgeneUS]

mihaild в сообщении #1693642 писал(а):

Например в игре "Алиса платит Бобу 1" цена игры ненулевая.

Можно подробнее, что имеется в виду?

mihaild в сообщении #1693642 писал(а):

И в данном случае я не вижу причин априори считать, что цена игры нулевая.

Нет, так нет. После записи выигрыша Боба, как у уважаемого worm2 или аналогично, видно, что если Алиса выигрывает, то Боб меняет стратегию, и Алиса проигрывает, и должна сменить стратегию.

Вообще говоря, мог быть случай: равновесие при проигрыше Алисы. Или вообще равновесие не достигается.
Много предположений делалось, и сильно повезло, что нашлось, так-то.

[mihaild]

EUgeneUS в сообщении #1693646 писал(а):

Можно подробнее, что имеется в виду?

Это контрпример к утверждению

EUgeneUS в сообщении #1693640 писал(а):

если равновесие Нэша существует, то при нём выигрыши сторон нулевые

У Алисы и Боба есть единственная стратегия, результат игры, если каждый выбирает свою единственную стратегию - Алиса платит Бобу 1.

[EUgeneUS]

Кстати, не факт, что найдены все стратегии в равновесии Нэша.

У Алисы, похоже, она единственная.
А вот у Боба не факт, что не существует других стратегий, при которых Алиса не может выиграть и обязана применять "нулевую стратегию".

-- 08.07.2025, 19:25 --

mihaild в сообщении #1693648 писал(а):

У Алисы и Боба есть единственная стратегия, результат игры, если каждый выбирает свою единственную стратегию - Алиса платит Бобу 1.

Я запутался
Можете подробнее описать эту игру?

[mihaild]

EUgeneUS в сообщении #1693650 писал(а):

Можете подробнее описать эту игру?

Неформально: Алиса платит Бобу 1. Всё.
Формально: у Алисы множество стратегий $\{a\}$, у Боба $\{b\}$, при профиле $\langle a, b\rangle$ у Алисы выигрыш $-1$, у Боба $+1$.

[EUgeneUS]

Теперь дошло, спасибо.