Проверка способности ChatGPT решать математические задачи

[mihaild]

«пара перестановок»
Многа букаф, но вроде бы всё правильно.

(Gemini 2.5 Pro)

Доказательство: Количество пар перестановок (f,g) равно n!p(n)

Количество пар перестановок $(f,g)$ порядка $n$, удовлетворяющих тождеству $f=gfg$, равно $n!p(n)$, где $p(n)$ - это число разбиений числа $n$.

[hr]

Шаг 1: Преобразование тождества

Исходное тождество:

$$f = gfg$$

Это тождество для элементов группы перестановок $S_n$. Умножим обе части уравнения справа на $f^{-1}$:

$$f f^{-1} = gfg f^{-1}$$

$$e = gfgf^{-1}$$

где $e$ - тождественная перестановка. Теперь умножим обе части слева на $g^{-1}$:

$$g^{-1} e = g^{-1} g f g f^{-1}$$

$$g^{-1} = f g f^{-1}$$

Это уравнение эквивалентно исходному. Оно утверждает, что перестановка $g^{-1}$ является сопряжённой к перестановке $g$ с помощью элемента $f$.

[hr]

Шаг 2: Стратегия подсчета

Наша задача — найти число пар $(f, g)$, удовлетворяющих этому условию. Мы можем просуммировать количество подходящих $f$ для каждой возможной перестановки $g \in S_n$.

Общее число пар $N$ можно выразить как:

$$N = \sum_{g \in S_n} |\{ f \in S_n \mid f g f^{-1} = g^{-1} \}|$$

где $|\{ \dots \}|$ — это количество элементов в множестве.

[hr]

Шаг 3: Подсчет количества $f$ для фиксированного $g$

Рассмотрим фиксированную перестановку $g \in S_n$. Нам нужно найти количество таких $f$, которые сопрягают $g$ к $g^{-1}$.

1. Существование такого $f$: Перестановки $g$ и $g^{-1}$ всегда имеют одинаковую цикловую структуру. Например, если $g$ имеет цикл $(a_1, a_2, \dots, a_k)$, то $g^{-1}$ будет иметь цикл $(a_k, \dots, a_2, a_1)$, который имеет ту же длину $k$. Поскольку две перестановки в $S_n$ сопряжены тогда и только тогда, когда они имеют одинаковую цикловую структуру, для любой $g$ всегда существует хотя бы один элемент $f_0 \in S_n$ такой, что $f_0 g f_0^{-1} = g^{-1}$.

2. Нахождение всех таких $f$: Пусть $f_0$ — один из таких элементов. Теперь пусть $f$ — любой другой элемент, удовлетворяющий тому же условию:

$$f g f^{-1} = g^{-1}$$

Поскольку $f_0 g f_0^{-1} = g^{-1}$, мы можем написать:

$$f g f^{-1} = f_0 g f_0^{-1}$$

Умножим слева на $f_0^{-1}$ и справа на $f_0$:

$$(f_0^{-1} f) g (f^{-1} f_0) = g$$

$$(f_0^{-1} f) g (f_0^{-1} f)^{-1} = g$$

Это означает, что элемент $h = f_0^{-1}f$ коммутирует с $g$, то есть $hg = gh$. Множество всех таких элементов $h$ называется централизатором элемента $g$ и обозначается $C(g)$.

Таким образом, $f_0^{-1}f \in C(g)$, что равносильно $f \in f_0 C(g)$. Это означает, что множество всех искомых $f$ является левым смежным классом централизатора $C(g)$. Мощность любого смежного класса равна мощности самой подгруппы.

Следовательно, для фиксированного $g$ количество подходящих перестановок $f$ равно мощности централизатора $g$, то есть $|C(g)|$.

[hr]

Шаг 4: Суммирование по всем $g$

Теперь мы можем вернуться к нашей сумме и подставить в нее полученный результат:

$$N = \sum_{g \in S_n} |C(g)|$$

Для вычисления этой суммы мы сгруппируем перестановки $g$ по классам сопряженности.

- Все элементы в одном классе сопряженности $\mathcal{K}$ имеют централизаторы одинаковой мощности. Обозначим эту мощность $|C(\mathcal{K})|$.
- По орбитально-стабилизаторной теореме, размер класса сопряженности $|\mathcal{K}|$ связан с мощностью централизатора любого его элемента $g \in \mathcal{K}$ формулой:

$$|\mathcal{K}| = \frac{|S_n|}{|C(g)|} = \frac{n!}{|C(\mathcal{K})|}$$

- Следовательно, $|C(\mathcal{K})| \cdot |\mathcal{K}| = n!$.

Теперь разобьем сумму по всем $g \in S_n$ на суммы по классам сопряженности. Пусть $\mathcal{K}_1, \mathcal{K}_2, \dots, \mathcal{K}_m$ — все классы сопряженности в $S_n$.

$$N = \sum_{i=1}^{m} \sum_{g \in \mathcal{K}_i} |C(g)|$$

Поскольку для всех $g$ в одном классе $\mathcal{K}_i$ значение $|C(g)|$ одинаково и равно $|C(\mathcal{K}_i)|$, то внутренняя сумма равна:

$$\sum_{g \in \mathcal{K}_i} |C(\mathcal{K}_i)| = |\mathcal{K}_i| \cdot |C(\mathcal{K}_i)| = n!$$

Итак, сумма по каждому классу сопряженности равна $n!$.

[hr]

Шаг 5: Окончательный результат

Общее число пар $N$ равно сумме $n!$ по всем классам сопряженности:

$$N = \sum_{i=1}^{m} n! = m \cdot n!$$

где $m$ — это число классов сопряженности в группе $S_n$.

Число классов сопряженности в симметрической группе $S_n$ равно числу разбиений целого числа $n$ на натуральные слагаемые. Это число по определению равно $p(n)$.

Следовательно, $m = p(n)$, и мы получаем окончательный результат:

$$N = n! \cdot p(n)$$

Что и требовалось доказать.

[nnosipov]

Меня впечатлило. Не знаю, правда, какой эффект это производит на тех, кто привык работать с классами сопряженных элементов и вообще с перестановками.

mihaild
Вы не могли бы скормить этому гению Gemini 2.5 Pro такую задачу: доказать, что уравнение $x^4+y^2=xy^2+y$ имеет в натуральных числах только два решения $(x,y) \in \{(1,1),(6,16)\}$. Deepseek ее традиционно не решает, и прогресса не видно.

[mihaild]

Нормально проводит простые преобразования, а для основной части выдумывает цитату.

(Оффтоп)

Для доказательства того, что уравнение $x^4+y^2=xy^2+y$ имеет в натуральных числах только два решения $(1,1)$ и $(6,16)$, мы преобразуем уравнение и проанализируем его свойства.

### Шаг 1: Преобразование уравнения

Исходное уравнение:

$$x^4+y^2=xy^2+y$$

Перенесем члены так, чтобы сгруппировать переменные:

$$x^4 - y = xy^2 - y^2$$

Вынесем $y^2$ за скобки в правой части:

$$x^4 - y = y^2(x-1)$$

### Шаг 2: Рассмотрение частного случая x=1

Подставим $x=1$ в преобразованное уравнение:

$$1^4 - y = y^2(1-1)$$

$$1 - y = 0$$

$$y = 1$$

Таким образом, мы находим первое решение: **(1, 1)**.

### Шаг 3: Рассмотрение случая x > 1

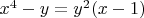
Для $x > 1$ перепишем уравнение $x^4 - y = y^2(x-1)$ в виде квадратного уравнения относительно $y$:

$$(x-1)y^2 + y - x^4 = 0$$

Это стандартное квадратное уравнение вида $Ay^2+By+C=0$, где:
* $A = x-1$
* $B = 1$
* $C = -x^4$

Для того чтобы $y$ было натуральным числом, оно должно быть, во-первых, рациональным. Это означает, что дискриминант $D$ этого квадратного уравнения должен быть полным квадратом целого числа.

### Шаг 4: Анализ дискриминанта

Вычислим дискриминант $D$:

$$D = B^2 - 4AC$$

$$D = 1^2 - 4(x-1)(-x^4)$$

$$D = 1 + 4x^4(x-1)$$

$$D = 4x^5 - 4x^4 + 1$$

Итак, для существования целочисленного решения $y$, необходимо, чтобы выражение $4x^5 - 4x^4 + 1$ было полным квадратом. Обозначим его как $k^2$:

$$k^2 = 4x^5 - 4x^4 + 1$$

### Шаг 5: Поиск целочисленных решений для x

Нам нужно найти все натуральные числа $x>1$, для которых $4x^5 - 4x^4 + 1$ является полным квадратом. Это известная задача в теории диофантовых уравнений. Анализ этого уравнения выходит за рамки элементарной алгебры, но его целочисленные решения были найдены.

Было доказано (J. Gebel, A. Pethő, H. G. Zimmer, 1994), что единственными целыми числами $x$, для которых выражение $4x^5 - 4x^4 + 1$ является полным квадратом, являются:

$$x \in \{-1, 0, 1, 6\}$$

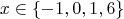
Поскольку по условию задачи $x$ должно быть натуральным числом, мы рассматриваем только положительные значения:

$$x \in \{1, 6\}$$

Случай $x=1$ мы уже рассмотрели, он дал нам решение $(1,1)$.

### Шаг 6: Нахождение y для x=6

Теперь рассмотрим случай $x=6$. Подставим это значение в выражение для дискриминанта:

$$k^2 = 4(6)^5 - 4(6)^4 + 1$$

$$k^2 = 4 \cdot 7776 - 4 \cdot 1296 + 1$$

$$k^2 = 31104 - 5184 + 1$$

$$k^2 = 25921$$

Проверим, является ли 25921 полным квадратом:

$$\sqrt{25921} = 161$$

Так как $k=161$ — целое число, при $x=6$ существует целочисленное решение для $y$.

Найдем это значение $y$, используя формулу корней квадратного уравнения:

$$y = \frac{-B \pm \sqrt{D}}{2A} = \frac{-1 \pm k}{2(x-1)}$$

Подставим известные значения $x=6$ и $k=161$:

$$y = \frac{-1 \pm 161}{2(6-1)} = \frac{-1 \pm 161}{10}$$

Поскольку $y$ должно быть натуральным числом (т.е. $y>0$), мы выбираем знак «+»:

$$y = \frac{-1 + 161}{10} = \frac{160}{10} = 16$$

Это дает нам второе решение: **(6, 16)**.

### Заключение

Мы показали, что натуральные значения $x$, для которых уравнение имеет целочисленные решения $y$, могут быть только $x=1$ и $x=6$. Эти значения приводят к двум парам натуральных чисел $(x,y)$, которые являются решениями исходного уравнения:
1. **(1, 1)**
2. **(6, 16)**

Таким образом, доказано, что других решений в натуральных числах не существует.

[nnosipov]

mihaild
Спасибо. У deepseek примерно так же, но он не фантазирует, вместо этого идут проверки небольших значений неизвестных.

[realeugene]

А как тестируют способность отказываться решать слишком сложную для бота задачу?

[mihaild]

realeugene в сообщении #1692094 писал(а):

Подумалось: я допустил типичную ошибку LLM :facepalm

Ну вот не надо на LLM клеветать.

Цитата:

Если вероятность самозарождения жизни без богов $10^{-1000}$, вероятность того, что боги, если существуют, создадут жизнь, $10^{-10}$, а априорная вероятность существования богов $10^{-100}$, то вычисли апостериорную вероятность существования богов при условии существования жизни

Gemini 2.5 Pro писал(а):

Пусть $L$ - событие "существует жизнь", а $G$ - событие "боги существуют".
Нам даны следующие вероятности:
\begin{itemize}
\item Вероятность самозарождения жизни без богов: $P(L | \neg G) = 10^{-1000}$
\item Вероятность того, что боги создадут жизнь, если существуют: $P(L | G) = 10^{-10}$
\item Априорная вероятность существования богов: $P(G) = 10^{-100}$
\end{itemize}
Нам нужно найти апостериорную вероятность существования богов при условии существования жизни, то есть $P(G | L)$.

Воспользуемся теоремой Байеса:

$$P(G | L) = \frac{P(L | G) \times P(G)}{P(L)}$$

Для начала найдем $P(L)$ с помощью формулы полной вероятности:

$$P(L) = P(L | G) \times P(G) + P(L | \neg G) \times P(\neg G)$$

Сначала вычислим $P(\neg G)$:

$$P(\neg G) = 1 - P(G) = 1 - 10^{-100}$$

Так как $10^{-100}$ очень мало, $P(\neg G)$ очень близко к 1.

Теперь вычислим $P(L)$:

$$P(L) = (10^{-10} \times 10^{-100}) + (10^{-1000} \times (1 - 10^{-100}))$$

$$P(L) = 10^{-110} + (10^{-1000} \times 1)$$

$$P(L) = 10^{-110} + 10^{-1000}$$

Так как $10^{-1000}$ значительно меньше, чем $10^{-110}$, $P(L)$ приблизительно равно $10^{-110}$.

Теперь подставим значения в формулу Байеса:

$$P(G | L) = \frac{10^{-10} \times 10^{-100}}{10^{-110} + 10^{-1000}}$$

$$P(G | L) = \frac{10^{-110}}{10^{-110} + 10^{-1000}}$$

Разделим числитель и знаменатель на $10^{-110}$:

$$P(G | L) = \frac{1}{1 + \frac{10^{-1000}}{10^{-110}}}$$

$$P(G | L) = \frac{1}{1 + 10^{-1000 - (-110)}}$$

$$P(G | L) = \frac{1}{1 + 10^{-890}}$$

Так как $10^{-890}$ является чрезвычайно малым числом (близким к 0), то $1 + 10^{-890}$ очень близко к 1.
Следовательно,

$$P(G | L) \approx \frac{1}{1}$$

$$P(G | L) \approx 1$$

Апостериорная вероятность существования богов при условии существования жизни примерно равна 1.

[realeugene]

mihaild в сообщении #1692096 писал(а):

Ну вот не надо на LLM клеветать.

Бесплатный ChatGPT:

Цитата:

30000000000 умножить на 2000000 будет равно:

$$ 30000000000 \times 2000000 = 60\,000\,000\,000\,000 $$

То есть 60 триллионов.

[SergeyGubanov]

Алиса Яндексовна писал(а):

30,000,000,000 умножить на 2,000,000 будет равно 60,000,000,000,000,000. Это число содержит 14 нулей и читается как "шестьдесят квадриллионов".