Спасибо! Я уже пробовал читать об этом, хотя это сейчас для меня не приоритетное направление, но вот, например:
Цитата:
Первый ординал — это

. Потом идет

. Следующий ординал — это

, потом

, и т. д. Дальше идет ординал "натуральные числа", который обозначают

. Если после всех натуральных чисел поставить самое большое число ...
Для непосвященного последнее предложение странно.
Для меня это тоже выглядит очень странно. Что это за "самое большое число", которое нужно поставить "после всех натуральных чисел"? Откуда Вы это взяли?
Вы хотите сказать, что эта теорема об именах чисел еще не доказана?
В арифметике нет теорем об именах, там есть только теоремы о числах. Объектами арифметики являются натуральные числа, а не их имена. Разумеется, равенство

в арифметике Пеано доказывается (прошу прощения, в моём
сообщении была опечатка, которую я сейчас исправил). Имена являются объектами метатеории.
Пусть нам дана совокупность

множеств

:

, где

, и при этом

.
Значит ли это, что речь здесь идет о двух одинаковых объектах
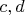
?
Предположение. Нет, речь здесь идет не о двух одинаковых объектах
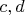
, а об одном и том же объекте

, который является одновременно элементом

множества

и элементом

множества

.
Это неверное предположение. На самом деле мы имеем один объект, которому мы по какой-то причине присвоили два разных имени "

" и "

", и только что Вы придумали для него ещё одно имя "

", так что теперь у нас

. Смысл этого равенства состоит в том, что мы во всех формулах можем свободно заменять имена "

", "

" и "

" друг на друга, не меняя смысла и логического значения формул. В частности, имеем полное право написать

или

. При этом множество

во всех трёх случаях будет одно и то же.
Но если под объектом иметь в виду не элемент множества, а то, что выступает в роли этого элемента?
Что значит "выступает в роли"? Если я говорю о числе

, то я имею в виду именно число

, а не нечто, "выступающее в роли числа

". И даже не строку "

", которая является одним из имён числа

.
В ролях элементов "

" и "

" выступает один и тот же объект, который я обозначил

Это просто один и тот же объект, и он выступает в роли самого себя.
а здесь он выступает в качестве элемента множеств

, где получает имена соответственно "

" и "

" -- то есть те же имена, что и соответствующие элементы
Что за "соответствующие элементы"? Имя элемента не должно зависеть от того, в каком множестве он содержится.
а также множества

, где ему, кстати, можно было бы дать третье имя, например,

, чтобы показать, что он является элементом еще одного множества, тогда было бы

По-моему, уже не третье, а четвёртое. Зачем размножать имена без необходимости? Вы хотите окончательно запутаться во всех этих многочисленных именах?
какие объекты он имеет в виду -- элементы "

" и "

" множеств

? Это ведь тоже объекты.
Строки "

" и "

" не являются элементами множеств

и

. Эти строки, конечно, являются объектами, но совершенно другой теории (метатеории).
У меня сложилось впечатление, что Вы не понимаете разницу между объектом и его именем. Надеюсь, хотя бы разницу между самим собой и своим именем Вы понимаете…