misha.physicsВы пишете, что хотите что-то читать научное, только не можете собраться. Это, наверное, потому, что у Вас нет в поле зрения хорошей книжки, которая была бы посильной и (тем самым) увлекла бы Вас. Хочу Вам предложить две книжки про тензоры. Они сложнее, чем то, что Вы до сих пор читали, однако, если Вам Будак-Фомин нормально пошел, есть надежда, что и несколько более высокий уровень Вы тоже освоите.
Жил такой большой математик и педагог,
Н.В.Ефимов. Он написал несколько известных хороших книжек. Последней была небольшая книжка
Введение в теорию внешних форм. Там очень подробно написано про внешнюю алгебру, дифференциальные формы и их интегрирование. Изложение очень аккуратное и последовательное, что называется, "дружественное к читателю". Всё весьма разжёвано. Надо оговориться, что я не могу дать голову на отсечение, что в этой книжке всё хорошо (он её писал будучи уже, что называется, в годах, но априори в общем доверяю репутации (в моих глазах) Ефимова как педагога).
Есть еще одна книжка.
T. Yokonuma, Tensor spaces and exterior algebra. Там с самого начала объясняется, очень подробно, "абстрактная" точка зрения на тензоры, что такое тензорное произведение и т.д. Но эта книга весьма
абстрактно-математична. К тому же она на иностранном языке. Впрочем, последнего не надо пугаться, ибо translated from Japan by T.Yokonuma. Проще говоря, он сам же её и перевел на английский, в силу чего и язык там весьма простой.
Но главное, и математичность, и английский язык у Йоконумы компенсируются крайней разжёванностью. По сравнению с Кострикин-Маниным там всё длиннее раза в три, а в начале так и вообще раз в пять. С моей точки зрения, из
существующих книжек по тензорам эта вообще лучшая. Я ссылку на нее когда-то увидел в одной статье, скачал, и она мне чрезвычайно понравилась, так что я ее уже не раз рекомендовал разным людям.
Такие вещи, как подъем/спуск индексов, а также звезда Ходжа, ни в Ефимове, ни в Йоконуме не объясняются, но если содержание этих книжек понять, то и с указанными вещами проблем не будет (они на самом деле просты).
-- 04.12.2018, 03:57 --(подъем, спуск, и Ходж)
Напишу уж прямо тут. Пусть у нас есть пространство

, и на нем невырожденная билинейная форма

, для простоты симметрическая. Тогда мы можем, используя эту форму, отождествить

с сопряженным пространством
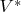
(вектор

соответствует линейной функции

, определяемой правилом

). Это стандартный факт из учебников (например, Кострикин, т.2, гл.3, пар.1, теорема 9).
Задача. Пусть  --- двумерное пространство с базисом
--- двумерное пространство с базисом  ,
, 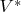 --- двойственное пространство,
--- двойственное пространство,  --- двойственный базис к
--- двойственный базис к  , и на
, и на  есть форма
есть форма  с матрицей
с матрицей  (т.е.
(т.е.  , и т.д.). Дан вектор
, и т.д.). Дан вектор  . Найдите соответствующий ему ковектор
. Найдите соответствующий ему ковектор  в базисе
в базисе  .
. (Сейчас решать не обязательно; написано, просто чтоб следующий абзац каким-то абстрактным не казался.)
Теперь, скажем, рассмотрим тензорное произведение

. Поскольку

отождествляется с
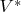
, то мы можем рассмотреть тензорное произведение тождественного отображения

и канонического изоморфизма

. Получается изоморфизм

. Это и есть то ли подъем, то ли спуск индексов. Если записать в координатах, то получатся известные формулы типа

.
(Не ожидайте, что Вы прямо сейчас поймете, что написано в этом абзаце. Это я Вам пишу на будущее, чтоб был мотив Йоконуму читать. Я могу обещать, что если Вы большую часть Йоконумы и Ефимова прочитаете, то написанное тут поймете).
Про Ходжа. Из формы

на

получается форма

на

, (

сомножителей), по правилу

. Далее, оказывается, что подпространство полностью антисимметричных тензоров, которое мы обозначим

, невырождено относительно формы. С другой стороны, есть билинейное отображение

(не что иное, как внешнее произведение форм). В силу того, что

одномерно, получается билинейное отображение из

в

.
Притом оно невырождено, и размерности у

и

одинаковы. Таким образом, двойственное пространство к

канонически изоморфно

. Но оно изоморфно и самому

, в силу невырожденности ограничения формы

. Поэтому получается некий канонический изоморфизм между

и

. Это и есть звезда Ходжа.
(то же самое: поймете с помощью указанных книжек. Не бог весть какая сложная вещь.)
Еще одно достоинство обоих книжек --- что там изложение идет сосредоточенно, без всяких уходов в сторону. А, например, "Современная геметрия" очень напоминает сборную солянку, там всё время изложение ветвится то туда, то сюда.
"Теория тензоров" как учебная область состоит, вообще говоря, из нескольких частей. Тут и тензорные произведения, и классическая алгебраическая теория тензоров (когда тензор рассматривается как табличка из

чисел), и
тензоры в криволинейных координатах, тензорные поля на многообразиях, интегрирование и теорема Стокса, и т.д. Поэтому предлагаемые книжки не отменяют других, "Современной геометрии" прежде всего, а служат для облегчения восприятия
их, как предварительное или параллельное чтение.
Другие книжки по тензорам с алгебраической точки зрения: Кострикин 2, Кострикин-Манин, Постников "Линейная алгебра".
Надо также иметь в виду, что в изложении в разных книжках могут быть разными "первичные понятия". В одних первичным понятием является тензор, а потом уже определяются пространства тензоров, тензорные произведения и т.д. В других же первично тензорное произведение пространств. Не удивляйтесь, что в разных книжках по разному. Я лично приверженец второго подхода.
Еще одна вещь. Книга Йоконумы (и вообще учение о тензорных произведениях) требует некоторого "алгебраического" мышления. И одновременно она же его и воспитывает. В частности, читая ее, вы можете познакомиться, неявно, с некоторыми "категорными" понятиями, типа: коммутативная диаграмма, универсальное свойство или объект, каноническое
или естественное отображение, канонический изоморфизм, естественное преобразование (возможно...). Чем это полезно ? Скажем, подъем-опускание индексов, и звезда Ходжа --- это как раз примеры естественных отображений. И имея в виду само это довольно "философское" понятие, легче воспринять данные конструкции. Короче, есть такие понятия, которые полезно иметь в виду.
Еще. Некоторые вопросы в Йоконуме можно пропустить, Вам они вряд ли нужны. А именно: тензорные произведения модулей над кольцами; расширение скаляров (полей) (часть (b) в пар.8 гл.1); большую часть гл.3.
(вроде всё ...)