Ну стыдно же так ошибаться, пиша пися творя учебное пособие.
Действительно, очень стыдно. С этим не поспорить...

Учебники так не пишутся не потому, что есть традиция писать их скучно, а из уважения автора к рабочему времени читателя.
Ну именно поэтому "учебником" я это и не называю. Изначально называл "методичкой", но это название у меня тоже не прижилось. "Креатифф" или нечто аналогичное, кмк, наиболее адекватное описание происходящего.
Сила не "организует движение", движение (равномерное прямолинейное) возможно и в отсутствие всяких сил.
Да, Вы правы. Хотя, строго говоря, отсутствие всяких сил -- это тоже вполне себе сила. Только нулевая.
И не думайте, что излагать основы просто. Кратко и понятно излагать что бы то ни было - тяжёлый труд, и тут надо серьёзно продумывать каждую формулировку по принципу "как бы быть понятным читателю и при этом ему не соврать".
Спасибо за критику. Постараюсь этому совету следовать в бОльшей степени.
Не стоит. А то нарветесь на кого-либо с несколько иными литературными вкусами.
Да, наверное и правда не стоит. К счастью/к сожалению, на английском приходится писать только специфического вида тексты, в которых подобное не очень идёт.
Обозначение

никак не поясняется,
Во, как раз по этому поводу у меня был вопрос. Я просто привык обозначать транспонирование плюсом, а сопряжение
\dagger. Естественно, на курсах линейки и т.п. транспонирование шло всегда через "T". И получается, что плюсовое обозначение нигде не употребляется, и я его сам себе выдумал?

а generic читатель понимать его не обязан
Я планировал по завершении сделать список обозначений в формулах. Наверное стоит его начать уже сейчас, и вести его параллельно с написанием, Вы правы.
Скорости то скалярные, то векторные, без пояснений - от этого у читателя могут поехать глаза и мозги.
Вроде же скаляры и векторы отличаются жирностью?
Извините, там такой объём работы, что первым редактором должны стать вы сами.
Конечно! Там ещё же далеко от завершения, я же об этом написал. Я просто закидываю удочку, чтобы потенциальный
Господин Редактор заранее высказал свои соображения по поводу правильности каких-то моментов. Естественно, лурковский стиль я отменять не буду, а по поводу устройства глав, расположения материала, качества иллюстраций и т.д. можно какие-то направления задать заранее.
Извините,

зависит в первую очередь от скоростей (

от них может тоже).
К своему очередному стыду, я не знал, что существует такая конвенция. Но она, очевидно, удобна. Обязательно возьму на вооружение!

Что-то я не уверен, что вариацией не называется линейная часть выписанного выражения (тогда она была бы аналогом дифференциала, а сейчас - аналог разности).
Спасибо Большое! Это как раз та самая штука, которую я уже один раз переписал, но плохо, и мысль о ней где-то на краю сознания витала, но вспомнить о ней никак не мог. Теперь с напоминанием о конкретном месте, я её наконец исправлю!
Что такое "оператор", и какие с ним правила обращения, не пояснено.
Про операторы написано же. Но Вы правы, надо дать ссылку, при упоминании наблы, на то место, где разбираются операторы.
-- 22.08.2018, 22:42 --Извините, в классической механике конфигурационным точно так же называется пространство
Спасибо большое, не знаю, почему у меня такая путаница с этим.

В разделе 3.2.2.7 (стр. 36-37) странно не упомянута некоммутативность
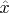
и

и связанная с этим неоднозначность квантования классических наблюдаемых.
Я очень хотел это написать там, но мне (почему-то) показалось логичным вынести это обсуждение в раздел по принципу неопределённости и по импульсному представлению. Это было осознанное и взвешенное решение, но, вероятно, неправильное.