Всем хорошего дня :)
Есть задача:
тело цилиндрической формы с толщиной стенок  м и диаметром и длиной
м и диаметром и длиной 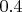 м падает с высоты
м падает с высоты  м со скоростью
м со скоростью  м/с. Нужно рассчитать изменение температуры цилиндра во время падения, если его начальная температура
м/с. Нужно рассчитать изменение температуры цилиндра во время падения, если его начальная температура  градусов, а температура среды -
градусов, а температура среды -  . Подсказка: нужно найти физические параметры стали и воздуха и воспользоваться теоремами Кондратьева. Ответ дать в виде графика
. Подсказка: нужно найти физические параметры стали и воздуха и воспользоваться теоремами Кондратьева. Ответ дать в виде графика  по пяти точкам
по пяти точкамСобственно, пытаюсь решать. Очевидно, что тело надо принять неподвижным, просто обдуваемым потоком воздуха со всех сторон со скоростью

м/с. Тело падает 40 секунд, поэтому точки - 8, 16, 24, 32, 40 секунды. Далее возникает соблазн воспользоваться теорией подобия, но в подсказке стоит использование теорем Кондратьева. Начинаю использовать. Нахожу критерий Био:

Критерий Био стремится к бесконечности, тепловой режим тела - стационарный. Формула темпа охлаждения:

, где

, а

, в свою очередь:

и

- объём и площадь поверхности тела, К - коэффициент формы тела, он посчитан и равен

.
Нахожу всё:

;

;

1/с.
Собственно, вопрос - а что делать дальше? Как узнать, какая температура будет у тела? Скорее всего, кстати, у меня в вычислениях ошибка, но это некритично, главное - понять алгоритм. Пытался вычислять температуру на следующей точке через формулу:

(ведь известно всё, кроме

), но ничего хорошего из этого не получилось.