это сопротивление заставляет меня делать те действия по решению, которые я сделал выше, для нахождения резонансной частоты
Дело в том, для поиска минимального

в данном случае не обязательно искать резонансную частоту. Достаточно заменить, что на резонансной частоте последовательного контура, какой бы она не была, сопротивление ветви

равно нулю. В общем-то достаточно очевидно, что тут и будет минимум

без громоздких формул.
Почему очевидно?
Других реактивных элементов нет, что сильно упрощает дело. На резонансной частоте параллельно

оказывается включена ветвь с нулевым сопротивлением. Ветвь с нулевым сопротивлением можно представить как перемычку. Если параллельно

включена перемычка, сопротивление

уже не имеет значения. Значит, всю цепь можно заменить на единственный оставшийся элемент.
Во всяком случае, такое умозрительное решение полезно проделать, прежде чем писать формулы. Если умозрительное решение Вам непонятно, тогда извиняюсь, что запутал :) Действуйте формальными методами, они тоже дадут ответ, но чуть более громоздко.
Тут я не понял для чего это все, минимум, производные, мои действия абсолютно не верны что ли?
Просят найти минимум

, то есть минимум модуля комплексного сопротивления. Как найти модуль комплексного числа, знаете? Если запишите формулу для

, мнимой части там уже не будет. Будет действительная функция от одной переменной

. У которой надо найти минимум. Проще, конечно, искать минимум у квадрата модуля, чтобы не заморачиваться к извлечением корня.
Я не говорил, что искать производную обязательно. Этот один из способов поиска минимума функции, который гарантированно работает при чисто механическом применении. Но часто минимум можно "увидеть" гораздо проще.
Как уже сказал
AnatolyBa, условие равенства нулю мнимой части

совпадает с условием минимума

только для частного случая. В общем случае может не совпадать. Например, рассмотрите функцию

нуль мнимой части будет при

, при этом
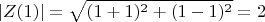
.
Однако, если взять

,

.