Лежит мешок, в нем очень много шаров, это что - все случайные величины?
Нет, это элементарные события.
Может опыты (вытаскивание шаров) - случайные величины?
Советую пользоваться не термином "элементарное событие", а "
исход" (потому как не всегда исходы являются событиями).
Таким образом, мешок с шарами - это
пространство  возможных исходов
возможных исходов 
.
Например, в нашем случае оно может быть записано так (если считать, что у нас в мешке четыре шара, каждый из которых обозначен уникальной буквой и имеет один из трех цветов - черный (black), белый (white) или красный (red)):

.
Наличие возможности фиксировать вхождение исхода (неважно, случайного или нет) в некоторые подмножества

(называемые
событиями), позволяет говорить о наличии некоей
алгебры событий 
.
Например, в нашем случае такими множествами (вхождение исхода в которые можно всегда установить) являются, очевидно,











...
(в общем, всевозможные множества, получающиеся из объединений множеств

(ну и пустое множество до кучи)).
Алгебра событий:

(Все эти множества соответствуют каким-то событиям, связанным с попаданием исхода в это множество. Например, попадание исхода в множество

можно понимать как наступление события "появившийся шар - черно-белый". Потому такое и название для множеств.)
Далее, если есть некоторое детерминированное (всегда одинаково действующее) правило, которое любому исходу ставит в соответствие число, и, что важно (хотя не в данном примере), есть возможность фиксировать попадание этого числа в любой числовой интервал (так называемая измеримость правила), то принято говорить о наличии
измеримой величины.
В нашем примере в качестве такого правила (такой измеримой величины) может быть выбрано, например, правило

, которое каждому шару в мешке ставит в соответствие

, если шар белый или черный, и

- если шар цветной (то есть, красный). Его можно записать как функцию:

, если

, иначе

.
Или, например, другое правило

, которое каждому шару ставит в соответствие порядковый номер буквы в алфавите:

, если

;

, если

;

, если

;

, если

.
Или, например, правило

, которое можно представить как:

.
(И вообще, делать всякие алгебраические комбинации этих функций, получая все новые).
Обращаю ваше внимание - до сих пор
НИГДЕ не предполагалось, что у нас есть какая-то случайность появления шаров из мешка - все сказанное подходит и в случае, когда из мешка вытаскивание производят совсем не случайно. Иными словами, понятие пространства исходов

, алгебры событий

и измеримой величины не требует наличия случайности! Двойку

принято называть
измеримым пространством (очевидно потому, что оно связано с измерением результатов исходов - неважно, случайных или нет).
А вот теперь, когда у нас есть измеримое пространство и измеримые величины, предположим, что мы обнаружили, что появление исходов мы
принципиально не можем предсказать, а можем только предсказать относительную (сколько раз попадает к общему числу наблюдений) частоту

попадания исхода во всякое множество

при очень большом числе наблюдений. Такую частоту называют
вероятностной мерой и обозначают

(обратите внимание, это функция от множества, а не от исхода), а тройку

-
вероятностным пространством.
Вот с ним и работает теория вероятностей, высчитывая значения

для одних событий, если знает их для других.
Измеримые величины на вероятностном пространстве принято называть
случайными величинами, но не потому, что они меняют свою природу (это как были детерминированные правила (функции), так и остались) - просто их значения начинают вычисляться для случайных исходов.
Значения случайной величины на конкретном исходе называется
реализацией случайной величины. Например, в нашем случае, если из мешка был вытащен шар

, то реализацией случайной величины

в этом случае будет число

, реализацией случайной величины

- число

, реализацией случайной величины

- число

.
(Хорошее правило - чтобы не путаться, обозначать случайные величины греческими буквами (или большими латинcкими), а их реализации - маленькими латинскими. Например,
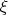
- случайная величина, а

- это ее реализация, то есть,

).
Далее, если смотреть только за появлением реализаций, например, случайной величины

и забыть о том, откуда эти числа берутся, то можно их начать воспринимать как исходы в новом, числовом, пространстве исходов

. На этом новом пространстве исходов тогда можно ввести новую алгебру событий (так называемую борелевскую алгебру

), тем самым получив новое измеримое пространство

, и наделить его вероятностной мерой

, соответствующей частоте появления тех или иных событий, связанных с реализацией случайной величины

, а именно, положить

Вероятностную меру

принято называть
распределением вероятностей (случайной величины  )
).
Например, в нашем случае, если шары вытаскивались равновероятно, то распределение вероятностей может быть представлено так:


, если борелевское множество

содержит в себе число

, но не содержит

;

- если не содержит

, но содержит

;

- если содержит и

и

;

- если не содержит ни

, ни

(Это не очень удобный способ представления распределения, потому используют другие -наиболее часто через функцию распределения

или ее плотность

).
Тогда получится новое, так называемое,
индуцированное случайной величиной  вероятностное пространство
вероятностное пространство 
. С ним проще работать, и при этом оно сохраняет всю информацию для вычисления вероятностей событий, связанных со случайной величиной

. Потому, если нас только эти события и интересуют - имеет смысл всегда работать с индуцированным пространством, а не исходным, что и делают большинстве случаев.
Как-то так. Хотя, конечно, чтобы это все хорошо осознать, надо повариться в этой теме, порешать задачки. Я привел лишь те моменты, которые принципиальны и позволяют привести голову в порядок, но при этом почему-то редко в такой явной форме встречаются в учебниках, в большинстве которых идет путанница, как и в примере с
--mS--, которая в высказываниях смешивала понятия "реализаций" и самих случайных величин, пока я не привел ей цитату из Wiki (и то, не признала свою ошибку).