К делу.
Решить неравенство:

. Поскольку
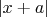
всегда положителен, мы должны найти все условия для параметра, когда выполняется отрицательность

. То есть, я так понимаю, иначе говоря, как мне подсказывает логика автора, просто решить это неравенство (
вот только надо его здесь вообще решить, я не понимаю... ведь какой бы мы не взяли параметр, разве он будет влиять на знак первого множителя?)
Итак,

На всякий случай, распишу получившиеся корни:

То есть имеем интервал

. Ну, следовательно, при другом неравенстве вовсе

.
Очевидно, ничего у меня здесь верного нет. Поэтому хотелось бы разобраться с вами, как решать подобные чудища. Например, с каких рассуждений начинать решение?