g______d, т.е. это то, что у Новикова и Тайманова в "Современных геометрических структурах и полях" называется ограничением на образ отображения?
Да, на странице 273 это объясняется, в том числе и гауссово отображение.
(Оффтоп)
Правда, я так и не понял, почему они обратный образ называют ограничением на образ; это же на самом деле перенос на прообраз. Кроме того, вводят эту операцию в точке (теорема 8.4), но не обсуждают, как она действует на тензорные или векторные поля. А это важный момент, в котором есть некоторая асимметрия: если

, то
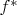
переносит

-формы с

на

. Но при этом нет естественного отображения, переносящего векторные поля с

на

. И наоборот,

индуцирует морфизм касательных расслоений

, но не индуцирует морфизма кокасательных расслоений ни в какую сторону.
Это связано с тем, что векторное поле — это одновременно "ко" и "контра" - объект. Это функция, т. к. точке сопоставляется вектор. Функции отображаются в обратную сторону. С другой стороны, это дифференцирование алгебры функций, поэтому должно отображаться в сторону, противоположную той, в которую отображаются функции. Поэтому отдельные касательные векторы отображаются в прямом направлении, а векторные поля нет: если

, то непонятно, какой из двух векторов брать в точке

: пришедший из точки

или из точки

.
С формами такого не возникает, т. к. там обе части отображаются в одну и ту же сторону.