Здравствуйте.
Помогите разобраться в решении 2х задач по мат.логике.
1) Пусть

- множество людей. На множестве

заданы следующие предикаты:
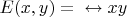
- один и тот же человек;
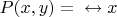
родитель

;
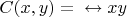
– супруги;
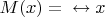
– мужчина;
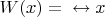
– женщина.
X – кузен.
Кузен - это двоюродный брат. Все кузены мужчины, значит
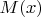
. У кузена могут быть дети, а может и не быть, т.е. есть такой

, для которого

является родителем
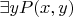
. Еще у кузена может быть жена, а может и не быть, т.е. есть такой

, для которого

является супругом
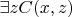
.
В итоге получается:
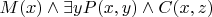
.
2) Привести формулу к предваренной форме:
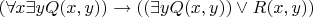
Избавляемся от импликации:
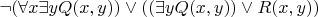
.
Перенос отрицания до формулы:
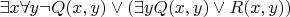
$[/math].
Замена переменной

во второй части выражения, т.к.

имеет связное и несвязное вхождение (чего быть не должно):
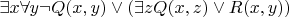
.
Вынос кванторов:
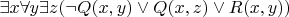
.
Просьба проверить и дать конструктивные комментарии.