provincialkaИ как это сделать? Ведь это множество до

, например, содержится в рациональной прямой
-- 09.10.2013, 21:45 --Пусть есть две прямые:

:

, где

и
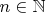
Отобразим на прямую

:

так, что

сопоставим

,
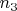
сопоставим

Тогда

можно перевести в какое-то рациональное число между

и

, верно?
-- 09.10.2013, 21:59 --Или я сейчас подумал...скажите пожалуйста, а при таком переходе сохраняется порядок?
И если, скажем, я напишу так:
1-ая прямая:

2-ая прямая:

(тут | - это, например, граничное иррациональное число какое-то)
это справедливо? Или это неверно/не очевидно?