Нет. Вам задали простой вопрос. Вот у вас есть фотон с совершенно конкретной волновой функцией, отвечающей определенному состоянию поляризации. Мы поставили перед ним повернутый на определенный угол поляризатор. Что увидит экспериментатор? Фотон пройдет через поляризатор? Нет? Если да, то почему. Если нет, то почему. Опишите результат количествено. Квантовая механика это позволяет. А вот ваше знание ее - не уверен...
Что увидит экспериментатор? Фотон пройдет через поляризатор?
Некорректный вопрос!
Корректно так. Поставим после поляризатора измеритель, который ловит фотон. Измеритель может показать экспериментатору 1 или 0. В случае 1 фотон пойман и экспериментатор
судит, что фотон прошел через поляризатор. В случае 0 экспериментатор может судить, что фотон либо не прошел через поляризатор либо проскочил мимо измерителя.
Ситуацию, что фотон проскочил мимо измерителя экспериментатор может исключить. Но это уже вторая еще не расписанная часть "теории" :). Будем считать, что фотон мог проскочить мимо измерителя.
Поляризатор будем считать идеальным. То есть, поляризатор можно описать как оператор

действующий на ВФ начального фотона

.

где

заданный угол поворота поляризатора.
Если экспериментатор точно знает ВФ измерителя и умеет решать ур-ние Шредингера для измерителя, то он может решить ур-ние для

и найти 1 или 0 выдаст измеритель. Допустил решение выдает 1.
Если он экспериментатор (если может :) мы не можем) поставит эксперимент с теми же исходными данными, то на выходе измерителя он получит 1.
Если ВФ фотона, ВФ измерителя точна не определена. Определен только угол поляризатора. Экспериментатор может задать для ВФ-ций статистический ансамбль всех возможных фотонов и всех возможных состояний измерителя. И искать теоретическую вероятность

, что измеритель выдаст 1.
Проведя множество реальных измерений экспериментатор найдет экспериментальную вероятность, отношение числа исходов с результатом 1 к числу исходов с результатом 0.
В силу эргодической гипотезы экспериментальная вероятность стремиться к теоретической.
(Оффтоп)
Как много букв. Не люблю расписывать :). и это только введение к задаче :(
Поскольку мы не умеем решать ур-ние Шредингера с измерителем, то предположим, что гипотеза квантовых измерений справедлива. В ней:
При этом P отношение числа решений с результатом измерения 1 к числу решений с результатом 0 равно интегралу от квадрата модуля ВФ на измерителе
То есть, теоретическая вероятность

равна:

разложим

по собственным функциям оператора




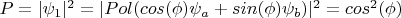 -- Сб июн 29, 2013 22:34:08 --
-- Сб июн 29, 2013 22:34:08 --(Оффтоп)
в учебники не заглядывал :). Обозначение оператора поляризации к сожалению не помню :(
myhand Задача решена? Ответ вас устраивает? :)
-- Сб июн 29, 2013 23:10:53 --Суть "проблемы" ТС - в другом. Ему кажется, что если волновая функция будет задана абсолютно точно - вероятности исчезнут
Правильно поняли :). Только в интерпретациях исчезнут. В принципах квантовой теории.
Это не так, для чего ему привели конкретный и элементарный пример
В расчетах вероятности исходов экспериментов, как есть так и будут.
Пример уж постарался разобрать :)