Добрый день уважаемые форумчане.
Возникли проблемы с решением задач на зачет.
Даны два вектора, вектор
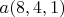
и вектор
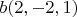
выходящие из одной точки. Найти вектор

, исходящий из той же точки, перпендикулярный вектору

, равный ему по длинне, компланарный с векторами

и

, и образующий с вектором

острый угол.