Соотношение неопределенностей на планковском масштабе имеет вид

где

- гравитационный радиус частицы,

- ее координата,

;

- фундаментальная планковская длина.
От него нетрудно перейти к соотношению неопределенностей Гейзенберга

Действительно, положим

и подставим соответствующие выражения для

и

. Получим

или, окончательно

Здесь

,

-- 4-скорость, равная единице, все остальные компоненты импульса для статического центрально-симметричного поля частицы равны нулю.
В квантовой механике известное соотношение неопределенностей

является полезным рабочим инструментом квантовой теории, позволяя довольно простым путем получать важные оценки. Аналогичным образом можно использовать установленное выше соотношение неопределенностей между гравитационным радиусом частицы

и координатой


В качестве примера рассмотрим выражение для пространственно-временной метрики

для центрально-симметричного гравитационного поля. В классической общей теории относительности оно имеет вид

Чтобы использовать это выражение на планковском масштабе, будем рассматривать величины

и

, входящие в него, как неопределенности соответственно гравитационного радиуса и координаты частицы. Согласно установленному выше соотношению неопределенностей, эти величины связаны друг с другом. Положим

, или проще

. Тогда

, а отношение

будет иметь вид

Используя это выражение, заменим величину

в метрике для

. Получим

Отсюда видно, что на планковском масштабе метрика пространства-времени ограничена снизу планковской длиной

. На этом масштабе материя (любая ее форма) переходит в чернодырное состояние, коллапсирует.
Аналогичным образом необходимо поступить и с другими выражениями, получаемыми в рамках общей теории относительности. Здесь мы, конечно, предполагаем, что канонические уравнения классической общей теории относительности сохраняют свой вид и на планковском масштабе.
В качестве еще одного примера рассмотрим движение частицы в центрально-симметричном гравитационном поле. Как и во всяком центральном поле, движение будет происходить в одной <<плоскости>>, проходящей через центр поля; выберем эту плоскость в качестве плоскости

. Воспользуемся уравнением Гамильтона-Якоби

где

-- масса частицы (массу же центрального тела обозначим здесь как

),

-- действие. С метрическим тензором

, где

-- гравитационный радиус центрального тела, это уравнение принимает вид

где

;

;

;

-- момент импульса.
Перепишем это уравнение следующим образом

Полученное уравнение является уравнением для энергии частицы, движущейся в центрально-симметричном гравитационном поле. Гравитационное поле здесь учтено наличием множителя

.
На планковском масштабе при качественном анализе этого уравнения мы можем подставить в него вместо величины

величину

, вместо импульса

величину

(исходя из условия квантования момента Бора), вместо момента импульса

величину

, где

,

-- главное квантовое число,

-- орбитальное квантовое число. Получим

Полученное уравнение можно отобразить и в форме графика для функции

, например, при

и постоянном значении

, причем точки пересечения графика с осью

, т.е. при

, будут характеризовать внешний (т. 1) и внутренний (т. 2) горизонты событий планковской черной дыры;

-- сингулярность.
С помощью анализа Эренфеста предыдущего уравнения можно построить аналогичные графики для функций

в пространствах с размерностями

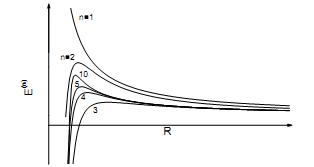
Из последнего рисунка видно, что максимумы кривых

в пространствах

,

лежат выше максимума кривой

в

. Это означает, что образование планковских черных дыр, с энергетической точки зрения, наиболее выгодно в

. Из рисунка видно, что планковские черные дыры могут образовываться и в пространствах других размерностей (кроме

), но минимальная полная энергия системы, необходимая для образования планковских черных дыр, присуща именно

-мерному пространству. В этом отношении трехмерное пространство выделено.
Всякая система стремится прийти в состояние с минимумом энергии, отдав при этом избыток имеющейся энергии. У системы, обладающей запасом энергии (возбужденной системы), всегда есть <<желание>> от нее избавиться, прийти в наинизшее энергетическое состояние. Системе это <<энергетически выгодно>>. Для пребывания в возбужденном энергетическом состоянии надо, чтобы была какая-то причина, мешающая системе освободиться от избытка энергии.
Если исходить из принципа, что любая физическая система стремиться реализоваться в состоянии с наименьшей энергией, то вполне очевидно, что, благодаря механизму образования планковских черных дыр в

- мерных пространствах и тому обстоятельству, что планковский вакуум лежит в основе наблюдаемого мира, выбор трехмерного пространства из всех других возможностей при формировании нашей Метагалактики был заранее предрешен.
Действительно, согласно современным представлениям, наблюдаемая Метагалактика возникла 13,7 млрд. лет тому назад из сингулярной <<точки>> с размером

см, то есть, согласно предыдущим выводам, наша Метагалактика появилась из <<чернодырного>> состояния физической материи. Отсюда с неизбежностью следует трехмерность наблюдаемого пространства.
С другой стороны, вакуум, согласно найденному выше соотношению неопределенностей, на планковском масштабе состоит из виртуальных планковских черных дыр, возникновение которых также энергетически наиболее выгодно в пространстве размерности три. Поэтому трехмерность наблюдаемого пространства (или четырехмерность пространства-времени) обусловлена исключительно <<кипением>> планковского вакуума. В планковских масштабах длин пустое пространство вовсе не является пустым - оно представляет собой вместилище самых бурных физических процессов. Причем эти процессы есть не что иное, как гравитационный коллапс, который непрерывно и всюду совершается, но вместе с тем совершается процесс, обратный коллапсу. Коллапс при планковском масштабе длин происходит всюду и непрерывно в виде квантовой флуктуации геометрии и, по-видимому, топологии пространства. В этом смысле коллапс постоянно протекает, но вместе с тем постоянно идет обратный процесс. Из всего вышеизложенного следует:
1. В микромире масштаб Планка является пределом расстояния.
2. При достижении масштаба Планка появляются планковские черные дыры, на планковском масштабе длин материя существует в чернодырном состоянии.
3. На планковском уровне вакуум состоит из виртуальных планковских черных дыр.
4. Ниже планковской длины операции измерения длины теряют смысл.
5. Трехмерность пространства является следствием энергетической выгодности образования планковского вакуума (виртуальных планковских черных дыр) на планковском масштабе.
Как можно видеть, на планковском масштабе энергий

такие гипотетические объекты, как <<струны>>. , <<браны>> и т.п., не должны существовать, однако это не исключает их наличие при масштабе энергий от

до

.
Понятно, что изложенный анализ не строг, но он нужен для понимания сути дела, и здесь его нельзя заменить никакими расчетами, даже самыми точными вычислениями. Такие расчеты не заменяют, а дополняют ясное понимание качественной стороны, понимание физического смысла явления. Физическая картина явления и его математическое описание дополнительны. Создание физической картины мира требует пренебрежения деталями и уводит от математической точности. И наоборот, попытка точного математического описания явления затрудняет ясное понимание. На вопрос «Что дополнительно понятию истины?» Бор ответил «Ясность».
Более полную информацию можно найти в статье
http://apklimets.narod.ru/Kvantovaja_gravitacia41.pdf