Кстати, в задаче число слагаемых ровно заданное

. А мы, если не ошибаюсь, решали задачу для всех разбиений…

Если
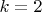
, то лучше чем на почти равные половины (

) не разбить, но это и так понятно.
(Оказывается, всё просто, хотя установил это не я. Впрочем, мой алгоритм всё равно остаётся применим, если не ошибаюсь.)