Я, пожалуй, тоже как-то более по теме выскажусь.
Интерактивные программы, и современные ОС как частный случай, не покрываются понятием вычислимой функции. Потому что они получают вход и выдают результат не "в одно действие".
Однако если отвлечься от некоторых деталей, их можно описать в рамках формализма теории рекурсии, в частности, формализма машин Тьюринга.
Во-первых, можно просто сказать, что когда порция выходных данных получена, мы просто запускаем машину еще раз с другими данными(которые могут зависеть от полученных). Получится игра с МТ в качестве игрока.
Во-вторых, если это удобно, то можно дать отдельное определение в духе интерактивной МТ. Например, так:
Имеется алфавит состояний машины

, алфавит ленты

, алфавит входных воздействий

, алфавит выходных воздействий

. У машины имеется головка с состоянием

, лента с ячейками с состояниями

, регистр входа с состоянием
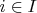
Программа - это последовательность команд вида

,
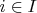
,

,

,

.
Действия

двигают головку ленты, действия из

печатают символ на текущей позиции, как обычно. Если же действие

было из алфавита

, то она выдает некоторое выходное воздействие и принимает новое входное, которое записывается в регистр.
Добавив еще немного очевидных формальностей, можно определить, каким образом программа для такой машины реализует функцию

или

, т.е. переводит последовательности (сколь угодно длинные или бесконечные, как нам больше нравится) входных воздействий в последовательности выходных.
Естественно, эта модель не учитывает многого, что в компьютере есть, но при определенных предположениях разумно описывает общее поведение, скажем, интерактивного commandline интерфейса, да и графического, наверное, тоже. Если хочется, можно добавить случайные числа и недетерминированность.
-- Чт авг 30, 2012 18:07:28 --Если хочется подчеркнуть интерактивность, то даже лучше рассматривать не

, а
