Ну-с, начнем с двумерия.
Рассмотрим в
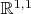
времениподобную кривую, заданную уравнениями
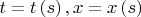
, где

- длина дуги.
Реализуем ориентацию сопутствующего репера гиперболическим поворотом.
Тогда вектор касательной есть
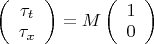
, а вектор нормали суть
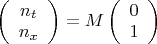
, где

имеет быть
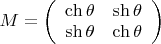
.
Угловая переменная

зависит от точки на кривой, т.е.
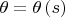
.
Как известно,
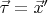
(штрихом будет обозначаться дифференцирование по

). Откуда
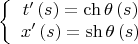
Вычислим теперь произведения вида
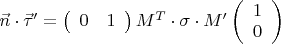
.
Здесь
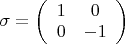
и её появлению мы обязаны псевдоэвклидовости.
Очевидно, для вычисления всех таких произведений достаточно вычислить внутреннюю матрицу
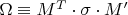
и обложить ее по-всякому единичковыми векторами слева и справа. То есть, означенная омега представляет из себя
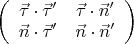
.
Вычисляем и имеем
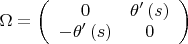
. Отсюда не трудно сообразить уравнения Френе:
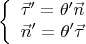
В случае постоянной кривизны
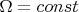
,
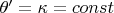
,
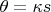
и
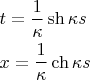
, то есть - псевдоокружность.
Ну, как-бы логично. Едем дальше...
Случай
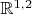
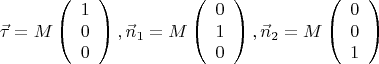
![$\[
M \equiv \left( {\begin{array}{*{20}c}
1 & 0 & 0 \\
0 & {\cos \varphi } & { - \sin \varphi } \\
0 & {\sin \varphi } & {\cos \varphi } \\
\end{array} } \right)\left( {\begin{array}{*{20}c}
{\operatorname{ch} \theta } & {\operatorname{sh} \theta } & 0 \\
{\operatorname{sh} \theta } & {\operatorname{ch} \theta } & 0 \\
0 & 0 & 1 \\
\end{array} } \right)\left( {\begin{array}{*{20}c}
1 & 0 & 0 \\
0 & {\cos \psi } & { - \sin \psi } \\
0 & {\sin \psi } & {\cos \psi } \\
\end{array} } \right)
\]
$ $\[
M \equiv \left( {\begin{array}{*{20}c}
1 & 0 & 0 \\
0 & {\cos \varphi } & { - \sin \varphi } \\
0 & {\sin \varphi } & {\cos \varphi } \\
\end{array} } \right)\left( {\begin{array}{*{20}c}
{\operatorname{ch} \theta } & {\operatorname{sh} \theta } & 0 \\
{\operatorname{sh} \theta } & {\operatorname{ch} \theta } & 0 \\
0 & 0 & 1 \\
\end{array} } \right)\left( {\begin{array}{*{20}c}
1 & 0 & 0 \\
0 & {\cos \psi } & { - \sin \psi } \\
0 & {\sin \psi } & {\cos \psi } \\
\end{array} } \right)
\]
$](https://dxdy-03.korotkov.co.uk/f/a/f/f/aff9b6e377cfed091052da70339877b582.png)
![$\[
\Omega \equiv M^T \cdot \sigma \cdot M'
\]
$ $\[
\Omega \equiv M^T \cdot \sigma \cdot M'
\]
$](https://dxdy-02.korotkov.co.uk/f/1/2/5/1252a8c3541e22b33d1d6b0ccbe7129b82.png)
, где теперь
![$\[
\sigma = \left( {\begin{array}{*{20}c}
1 & 0 & 0 \\
0 & { - 1} & 0 \\
0 & 0 & { - 1} \\
\end{array} } \right)
\]
$ $\[
\sigma = \left( {\begin{array}{*{20}c}
1 & 0 & 0 \\
0 & { - 1} & 0 \\
0 & 0 & { - 1} \\
\end{array} } \right)
\]
$](https://dxdy-02.korotkov.co.uk/f/9/c/9/9c997d62cac764bbaa430a598ea9d31782.png)
.
После несколько нудноватых (или отданных кумпутеру) вычислёвываний, поимеем
![$\[
\Omega = \left( {\begin{array}{*{20}c}
0 & {\kappa _1 } & \delta \\
{ - \kappa _1 } & 0 & {\kappa _2 } \\
{ - \delta } & { - \kappa _2 } & 0 \\
\end{array} } \right)
\]
$ $\[
\Omega = \left( {\begin{array}{*{20}c}
0 & {\kappa _1 } & \delta \\
{ - \kappa _1 } & 0 & {\kappa _2 } \\
{ - \delta } & { - \kappa _2 } & 0 \\
\end{array} } \right)
\]
$](https://dxdy-04.korotkov.co.uk/f/7/5/5/75520a8342222d0ac96a69d9ef418be682.png)
,
где
![$$\[
\begin{gathered}
\kappa _1 = \cos \psi \cdot \theta ' + \sin \psi \cdot \operatorname{sh} \theta \cdot \varphi ' \hfill \\
\kappa _2 = \operatorname{ch} \theta \cdot \varphi ' + \psi ' \hfill \\
\delta = - \sin \psi \cdot \theta ' + \cos \psi \cdot \operatorname{sh} \theta \cdot \varphi ' \hfill \\
\end{gathered}
\]
$$ $$\[
\begin{gathered}
\kappa _1 = \cos \psi \cdot \theta ' + \sin \psi \cdot \operatorname{sh} \theta \cdot \varphi ' \hfill \\
\kappa _2 = \operatorname{ch} \theta \cdot \varphi ' + \psi ' \hfill \\
\delta = - \sin \psi \cdot \theta ' + \cos \psi \cdot \operatorname{sh} \theta \cdot \varphi ' \hfill \\
\end{gathered}
\]
$$](https://dxdy-02.korotkov.co.uk/f/5/e/3/5e3aa965a171a40eeceaaa46d761ff9482.png)
Пару слов о

. Приблуда сия образовалась оттого, что в общем случае мы не совсем попали первой нормалью в направление производной касательной. Чтобы попасть совсем, надобно эту дельту обнулить. Что даст нам связь и оставит из трех только два параметра, определяющих направление касательной. Собственно, как и должно быть.
Таким образом, нужно решить систему
![$\[
\kappa _1 = const,\kappa _2 = const,\delta = 0
\]
$ $\[
\kappa _1 = const,\kappa _2 = const,\delta = 0
\]
$](https://dxdy-02.korotkov.co.uk/f/1/4/d/14d49fc3c18136c8120702bc05c8ea1482.png)
, получить из нее
![$\[
\varphi = \varphi \left( s \right),\theta = \theta \left( s \right),\psi = \psi \left( s \right)
\]
$ $\[
\varphi = \varphi \left( s \right),\theta = \theta \left( s \right),\psi = \psi \left( s \right)
\]
$](https://dxdy-02.korotkov.co.uk/f/5/9/6/596d28de6f679aa79100298135ff563d82.png)
, подставить сие в
![$\[
t'\left( s \right) = \operatorname{ch} \theta \left( s \right),x'\left( s \right) = \cos \varphi \left( s \right) \cdot \operatorname{sh} \theta \left( s \right),y'\left( s \right) = \sin \varphi \left( s \right) \cdot \operatorname{sh} \theta \left( s \right)
\]
$ $\[
t'\left( s \right) = \operatorname{ch} \theta \left( s \right),x'\left( s \right) = \cos \varphi \left( s \right) \cdot \operatorname{sh} \theta \left( s \right),y'\left( s \right) = \sin \varphi \left( s \right) \cdot \operatorname{sh} \theta \left( s \right)
\]
$](https://dxdy-01.korotkov.co.uk/f/0/9/f/09ff1a85de2548db7a1b418992b6195e82.png)
(пси, кстати, выпало) и, проинтегрировав еще раз, получить наконец кривулю.
Этого я пока не добил. Нашел только интеграл
![$\[
\sin \psi = \frac{{c_1 + \kappa \operatorname{ch} \theta }}
{{\operatorname{sh} \theta }}
\]
$ $\[
\sin \psi = \frac{{c_1 + \kappa \operatorname{ch} \theta }}
{{\operatorname{sh} \theta }}
\]
$](https://dxdy-01.korotkov.co.uk/f/8/6/f/86feadd97b4dda009515685b61350e7982.png)
, где
![$\[
\kappa \equiv \frac{{\kappa _2 }}
{{\kappa _1 }}
\]
$ $\[
\kappa \equiv \frac{{\kappa _2 }}
{{\kappa _1 }}
\]
$](https://dxdy-01.korotkov.co.uk/f/0/a/0/0a093484c11c4aedb64ade0c1dc5c35d82.png)
, а
![$\[
{c_1 }
\]
$ $\[
{c_1 }
\]
$](https://dxdy-02.korotkov.co.uk/f/5/6/1/561553ef6358617c7ded2cd559c0df3482.png)
- еще одна постоянная. Да свёл её к более простому виду
![$\[
\varphi ' = \kappa _1 \frac{{\sin \psi }}
{{\operatorname{sh} \theta }},\theta ' = \kappa _1 \cos \psi
\]
$ $\[
\varphi ' = \kappa _1 \frac{{\sin \psi }}
{{\operatorname{sh} \theta }},\theta ' = \kappa _1 \cos \psi
\]
$](https://dxdy-04.korotkov.co.uk/f/3/4/2/342bbd95ae70e8fa0f6a165a0cf3f42682.png)
.
Вот примерно как-то вот так вот.
P.S. Чтобы двинуть далее с песнями на
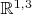
, надо как-то обобщить на четырехмерие углы Эйлера. Кто-то знает за такое стандартное или отсебятину тулить?