В итоге,
по первой задаче, получилось:
-- исправлено --![$f(A) \in K[A]$ $f(A) \in K[A]$](https://dxdy-01.korotkov.co.uk/f/4/d/b/4db6fb279ff18dc608f36d6dc8830e8182.png)
, где
![$K[A]$ $K[A]$](https://dxdy-02.korotkov.co.uk/f/5/0/e/50e65edc0a51af234bc1ff3c589af91582.png)
- кольцо матричных многочленов действующих на

.
Тогда условие

означает, что

Далее, оператор

- нормальный, т.е.

и

. Поэтому

. Следовательно условие

влечет равенство

или, что эквивалентно,

, что и требовалось доказать
По второй:Доказываем индукцией по размеру матрицы.
Для

и

утверждение очевидно.
Пусть утверждение верно для всех

и пусть

- матрица размера

.
Отметим элемент
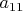
и дополнительный к нему главный минор

.
Поскольку матрица

симметричная, она может быть приведена к диагональному виду некоторым ортогональным преобразованием.
Рассмотрим такое преобразование

.
Здесь ортогональная матрица

имеет следующий блочно-диагональный вид:
В левом верхнем углу стоит 1, а дополнительным к ней блоком является ортогональная матрица

, приводящая минор

к диагональному виду

Тогда будем иметь

, что и требовалось доказать
Вроде все верно, если есть какие то ошибки и неточности, или что-то в докзательстве неочевидно - прошу сообщить.