Премия за бесконечность

[EEater]

Так называется заметка в сегодняшнем номере АиФ. Аналогичные сообщения появились и в других СМИ, вот, например, из РГ:

Цитата:

Доктор физико-математических наук Ярослав Сергеев стал лауреатом международной премии Пифагора, которой отмечаются крупные достижения в области математики. Награда вручена в итальянском городе Кротон.
Премия вручена за... бесконечность. Она всегда интересовала математиков, но не удавалось создать аппарат, который бы позволил оперировать бесконечно большими или бесконечно малыми величинами. Ярослав Сергеев создал новый математический язык, новую арифметику. С ее помощью с бесконечностями можно выполнять обычные операции: складывать и вычитать, делить и умножать. Кроме того, он запатентовал в России, Европейском союзе и США "компьютер" бесконечности. Собственно он и дает возможность проводить столь необычные вычисления.

Не может ли кто-то из профи прокомментировать информацию?

[shwedka]

Событие истинное. Я несколько дней назад видела это сообщение на сайте университета Калабрии, который эту премию присуждает.
Действительно, приз Пифагора ранее присуждался ООООчень видным людям.
Сергеев, работает в том же университете, весьма заштатном. В его пользу нужно отметить, что итальнцы крайне неохотно берут на работу неевропейких иностранцев, даже весьма заслуженных.
Сергеев имеет прекрасныю репутацию в области глобальной оптимизации. Приглашенные доклады на видных конференциях, профессиональные призы, много публикаций в непоследних журналах.
вопросами 'бесконечности' начал заниматься лет 5 назад. Публикации, немногие,какие есть, носят оттенок научпопа, с изрядной саморекламой. Я посмотрела кое что, впечатление (мое и некоторых других)-- как несколько изуродованный и плохо изложенный нестандартный анализ. 'Компьютер бесконечности', якобы сконструированный - чисто теоретическое измышление, типа машины Тьюринга. Считать на нем никогда не будут. Но для рекламы звучит хорошо.

История появления сообщение. Первое в России- на сайте его родного университета, в Н.Новгороде. Скорее всего, им инспирированное. На день позже появилось на 'Русском радио' -- и только в последние пару дней растеклось по русской медиа. Без новой информации.

В целом, мое мнение, здесь немалая доза прохиндейства со стороны сильного ученого. Ему не хватило нормальной профессиональной деятельности, и он взлетел на бесконечности. Ну, как Фоменко со своей историей. Присуждение премии, видимо, связано с тем, что им хотелось наградить кого-то местного, своих не нашлось, а тут Сергеев со своей хорошо зарекламированной бесконечностью подъехал.
В цлом, теперь список награжденных выглядит как 'Гомер, Мильтон и Паниковский'.

Кому сильно интересно, могу дать ссылки на публикации.

[EEater]

shwedka, спасибо за исчерпывающий комментарий! Мне тоже сходу подумалось, что пахнет нестандартным анализом.
В самом деле, если есть ссылочка именно на работу (-ы) по тематике, о которой идет речь - не откажите привести.

-- Ср ноя 10, 2010 17:07:42 --

Нашел в интернете "аксиоматику" теории со ссылкой на "Троицкий вариант".

Цитата:

Постулат 1. Существуют бесконечные и бесконечно малые объекты, но люди и машины могут совершать только конечное число операций.
Постулат 2. Не обсуждается то, чем являются математические объекты, с которыми мы работаем; мы только конструируем более мощные средства, которые позволяют нам усовершенствовать наши возможности наблюдать и описывать математические объекты.
Постулат 3. Принцип, сформулированный древними греками, – «часть меньше целого», – применяется ко всем числам (конечным, бесконечным и бесконечно малым) и ко всем множествам и процессам.

На математику не похоже совсем...

[shwedka]

Sergeyev, Yaroslav D. Counting systems and the first Hilbert problem. Nonlinear Anal. 72 (2010), no. 3-4, 1701–1708,
Sergeyev, Yaroslav D. Numerical point of view on calculus for functions assuming finite, infinite, and infinitesimal values over finite, infinite, and infinitesimal domains. Nonlinear Anal. 71 (2009), no. 12, e1688–e1707
Sergeyev, Yaroslav D. Numerical computations and mathematical modelling with infinite and infinitesimal numbers. J. Appl. Math. Comput. 29 (2009), no. 1-2, 177–195,
Sergeyev, Yaroslav D. A new applied approach for executing computations with infinite and infinitesimal quantities. Informatica (Vilnius) 19 (2008), no. 4, 567–596,
Sergeyev, Yaroslav D. Mathematical foundations of the infinity computer. Ann. Univ. Mariae Curie-Skłodowska Sect. AI Inform. 4 (2006), 20–33.
Sergeyev, Yaroslav D. Arithmetic of infinity. Edizioni Orizzonti Meridionali, Cosenza, 2003. viii+104 pp. ISBN: 88-89064-01-3

Две на уровне самиздата, еще две в журнале Nonlinear Anal, который славится в последнее время тем, что по причине неквалифицированного рецензирования иногда публикует чушь, за которую потом краснеет. А стиль, да, научпоп с манией величия. Занимался бы своей оптимизацией.
Вот что пишут специалисты

The book starts with a rather standard description of infinity in mathematics. First, the author provides a detailed description of the peculiar properties of infinite sets—like Galileo's "paradox'' that, on one hand, there are exactly as many squares as natural numbers, but, on the other hand, not every natural number is a square, so there should be fewer squares than natural numbers. Then, the author describes the traditional Cantor arithmetic of cardinal and ordinal numbers. In Chapter 3, he describes his own approach to infinity, an approach that is free of "paradoxes'' like Galileo's (and thus, in better accordance with common sense). 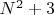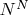In this approach, the author starts with a fixed "infinite number'' $N$ that is divisible by all natural numbers, and then considers expressions containing $N$, such as $N+1$, $N^2+3$, $N^N$, etc., as different infinite numbers.
The author presents this as a completely new idea, but readers familiar with non-standard analysis will immediately recognize that the resulting set is a (kind of) non-standard extension of natural numbers, with $N$ an infinitely large (non-standard) integer.
V. Ya. Kreinovich

[maxal]

Вот здесь "разбор полётов" отнюдь не лестный для Сергеева: http://knop.livejournal.com/193343.html

См. также статью
Гутман А. Е., Кутателадзе С. С. О теории гросс-единицы. Сибирский математический журнал 49(5), 2008, с. 1054-1076.

и комментарий Кутателадзе в свежем Троицком варианте (стр. 3)

-- Wed Nov 10, 2010 11:58:34 --

Популярно идеи Сергеева были изложены в Компьютерре еще 3 года назад:
http://www.computerra.ru/think/332773/

[shwedka]

Появился посвященный Сергееву язвительный препринт Кутателадзе,
http://www.math.nsc.ru/LBRT/g2/english/ssk/preprint250.pdf

[maxal]

shwedka в сообщении #377933 писал(а):

Появился посвященный Сергееву язвительный препринт Кутателадзе,
http://www.math.nsc.ru/LBRT/g2/english/ssk/preprint250.pdf

Там рядом еще целая страничка с различными ссылками по теме: http://math.nsc.ru/LBRT/g2/english/ssk/crook.html

[Dan B-Yallay]

Где можно узнать о том, как в 60-е годы солидные учёные восприняли идеи Нестандартного Анализа?

[shwedka]

Dan B-Yallay
Напишите Кутателадзе. Или есть немного во введении к его книге 'Нестандартные методы анализа'

[Dan B-Yallay]

shwedka
Спасибо.

[Кардановский]

swedka: Должен признаться: крайне неприятно удивлен таким вот ругательным характером нападок на лауреата престижной международной премии! Скажите,а примут ли ваше оппонирование Сергееву в тех солидных журналах,где его публикуют? Пытались ли вы своим авторитетом разубедить международный комитет,присудивший ему премию?

[shwedka]

Кардановский в сообщении #379877 писал(а):

swedka:

Могли бы Вы быть повнимательнее и скопировать мой ник без ошибок. Или это специально? В порядке хамства?

Кардановский в сообщении #379877 писал(а):

на лауреата престижной международной премии!

Премия престижной не является.
Премия была дана городом Кротон без согласования с Итальянским математическим союзом или какой-либо иной официальной математической организацией Италии...

Кардановский в сообщении #379877 писал(а):

Скажите,а примут ли ваше оппонирование Сергееву в тех солидных журналах,где его публикуют?

Потуги о 'бесконечности' напечатаны в крайне несолидных изданиях. Практически, самиздат.

Кардановский в сообщении #379877 писал(а):

международный комитет,присудивший ему премию?

'Международный комитет' состоит из отставного лицейского учителя, журналиста и коллеги Сергеева по кафедре и по глобальной оптимизации. все итальянцы.

Если, между проим, почитаете мой первый пост, то увидите, что я не отрицаю заслуг Сергеева в его основной тематике.

А с чего Вы так бросились на его защиту? Вы прочитали его труды?

[Dandan]

Кардановский в сообщении #379877 писал(а):

swedka: Должен признаться: крайне неприятно удивлен таким вот ругательным характером нападок на лауреата престижной международной премии! Скажите,а примут ли ваше оппонирование Сергееву в тех солидных журналах,где его публикуют? Пытались ли вы своим авторитетом разубедить международный комитет,присудивший ему премию?

премии, публикации и заявления "авторитетов" не являются доказательством правильности или уникальности утверждений. Это математика.

[Кардановский]

Мне показалось,что"shwedka" - это неправильно! "Шведка" по-шведски будет "svenska". Поэтому я просто попытался несколько приблизить ваш ник к правильному шведскому или английскому "swede" - только то и всего! Впрочем,может быть и такое,что вы и не из Швеции вовсе...На форумах то ведь каждый волен представляться кем захочет и откуда захочет...
Что касается трудов Сергеева или кого-либо еще (Иванова,Свенсона,Рабиновича и др.),то,на мой взгляд, оппонирование должно строиться по-существу содержания этих работ. Если в них есть изъяны,то доказательно укажите какие. Так это принято у математиков и не только у них... Одними эмоциональными проявлениями симпатий или антипатий в хорошей академической дискуссии по математике аргументировать недопустимо... В общем,как видите,вовсе не в личности Сергеева и не в содержании его трудов причина моего вмешательства в это обсуждение...

[shwedka]

Кардановский в сообщении #380100 писал(а):

Что касается трудов Сергеева или кого-либо еще (Иванова,Свенсона,Рабиновича и др.),то,на мой взгляд, оппонирование должно строиться по-существу содержания этих работ.

Стало быть, от претензий ко мне по поводу качества журналов, престижности премии или квалифицированности присуждающего комитета Вы отказываетесь? Прекрасно, запишем, хотя приличнее было бы этот отказ сформулировать явно.

Кардановский в сообщении #380100 писал(а):

Мне показалось,что"shwedka" - это неправильно!

Мне показалось, что я не давала Вам полномочий исправлять выбранный мною мой ник, даже если у ВАс есть некоторые познания в шведском. У меня, скажем, тоже могут возникнуть сомнения в правильности написания Вашей фамилии и мнения о том, как ее правильно писать. Вам интересно?

Кардановский в сообщении #380100 писал(а):

Если в них есть изъяны,то доказательно укажите какие.

ПО-моему, maxal и я дали достаточное количество ссылок на содержательное обсуждение сергеевской бесконечности, чтобы защитить нас от обвинений в их отсутствии. Ваше рвение встать на его защиту похвально, но было бы весомее, будучи поддержано содержательными доводами в его пользу.