Функция, непрерывная в рац. точках и разрывная в иррациональ

[Freez[e]]

Народ подскажите как доказать что не существует функции по свойствам обратным функции Римана....
Функция Римана непрерывна в каждой иррациональной точке отрезка и разрывна в каждой его рациональной точке.
При иррацион f(x)=0
при рацион f(x)=1/n где m/n - рац. число....

[Someone]

Freez[e] писал(а):

Народ подскажите как доказать что не существует функции по свойствам обратным функции Римана....
Функция Римана непрерывна в каждой иррациональной точке отрезка и разрывна в каждой его рациональной точке.
При иррацион f(x)=0
при рацион f(x)=1/n где m/n - рац. число....

Под "обратными свойствами" подразумевается, что функция должна быть непрерывной во всех рациональных точках и разрывной во всех иррациональных?

Предположим, что на числовой прямой $\mathbb{R}$ задана функция $f(x)$, которая имеет всюду плотное множество точек непрерывности.

Возьмём любое натуральное число $n\in\mathbb{N}$ и определим множество $U_n$ как объединение всех интервалов $(a,b)\subseteq\mathbb{R}$, удовлетворяющих следующему условию: для любых $x,y\in(a,b)$ выполняется неравенство $|f(x)-f(y)|<\frac{1}{n}$.

Множество $U_n$, очевидно, открыто; кроме того, оно является всюду плотным, так как содержит множество точек непрерывности функции $f(x)$. Поэтому дополнительное множество $F_n=\nathbb{R}\setminus U_n$ замкнуто и нигде не плотно на числовой прямой $\mathbb{R}$.

Пересечение всех множеств $U_n$, разумеется, совпадает с множеством точек непрерывности функции $f(x)$, в то время как множество точек разрыва является объединением счётного семейства нигде не плотных множеств $F_n$, $n\in\mathbb{N}$, то есть, множеством первой категории.

Поскольку по теореме Бэра множество иррациональных чисел не является множеством первой категории, оно не может быть множеством точек разрыва никакой функции, определённой на всей числовой прямой $\mathbb{R}$.

P.S. Судя по предварительному просмотру, трансляция TeX-овских формул отлажена плохо: одно и то же выражение \mathbb{R} дало три разных шрифта. А \frac{1}{n} вообще дало какую-то ерунду, пришлось написать 1/n.

P.P.S. Спасибо за подсказку. Но я был уверен, что тег {math}{/math} знаки доллара заменяет.

[cepesh]

Вот что получится, если писать {math}$</span><!-- b end -->...<span style={/math}

Под "обратными свойствами" подразумевается, что функция должна быть непрерывной во всех рациональных точках и разрывной во всех иррациональных?

Предположим, что на числовой прямой $\mathbb{R}$ задана функция $f(x)$, которая имеет всюду плотное множество точек непрерывности.

Возьмём любое натуральное число $n\in\mathbb{N}$ и определим множество $U_n$ как объединение всех интервалов $(a,b)\subseteq\mathbb{R}$, удовлетворяющих следующему условию: для любых $x,y\in(a,b)$ выполняется неравенство $|f(x)-f(y)|<1/n$.

Множество $U_n$, очевидно, открыто; кроме того, оно является всюду плотным, так как содержит множество точек непрерывности функции $f(x)$. Поэтому дополнительное множество $F_n=\nathbb{R}\setminus U_n$ замкнуто и нигде не плотно на числовой прямой $\mathbb{R}$.

Пересечение всех множеств $U_n$, разумеется, совпадает с множеством точек непрерывности функции $f(x)$, в то время как множество точек разрыва является объединением счётного семейства нигде не плотных множеств $F_n$, $n\in\mathbb{N}$, то есть, множеством первой категории.

Поскольку по теореме Бэра множество иррациональных чисел не является множеством первой категории, оно не может быть множеством точек разрыва никакой функции, определённой на всей числовой прямой $\mathbb{R}$.

[cepesh]

А вот что получится, если все загнать под {math}, окружив формулы $$:
http://lib.mexmat.ru/math/9643904e56a12 ... 285b50.png

[math]Под "обратными свойствами" подразумевается, что функция должна быть непрерывной во всех рациональных точках и разрывной во всех иррациональных?

Предположим, что на числовой прямой $\mathbb{R}$ задана функция $f(x)$, которая имеет всюду плотное множество точек непрерывности.

Возьмём любое натуральное число $n\in\mathbb{N}$ и определим множество $U_n$ как объединение всех интервалов $(a,b)\subseteq\mathbb{R}$, удовлетворяющих следующему условию: для любых $x,y\in(a,b)$ выполняется неравенство $|f(x)-f(y)|<1/n$.

Множество $U_n$, очевидно, открыто; кроме того, оно является всюду плотным, так как содержит множество точек непрерывности функции $f(x)$. Поэтому дополнительное множество $F_n=\nathbb{R}\setminus U_n$ замкнуто и нигде не плотно на числовой прямой $\mathbb{R}$.

Пересечение всех множеств $U_n$, разумеется, совпадает с множеством точек непрерывности функции $f(x)$, в то время как множество точек разрыва является объединением счётного семейства нигде не плотных множеств $F_n$, $n\in\mathbb{N}$, то есть, множеством первой категории.

Поскольку по теореме Бэра множество иррациональных чисел не является множеством первой категории, оно не может быть множеством точек разрыва никакой функции, определённой на всей числовой прямой $\mathbb{R}$.[/math]

[Freez[e]]

Коротко но есть непонятные моменты...
разъясните неродивому перваку
1) почему все точки х и у должны удовлетворять |f(x)-f(y)|<1/n ??
2) если можно дайте док-во для иррациональных чисел, сто они не образуют множества перыой категории

[Someone]

Freez[e] писал(а):

Коротко но есть непонятные моменты...
разъясните неродивому перваку
1) почему все точки х и у должны удовлетворять |f(x)-f(y)|<1/n ??
2) если можно дайте док-во для иррациональных чисел, сто они не образуют множества перыой категории

1) Прежде всего, я нигде не говорил, что все точки $x$ и $y$ удовлетворяют этому неравенству. Я говорил об объединении интервалов, все точки которых удовлетворяют этому неравенству. Такие интервалы существуют всегда, когда функция имеет точки непрерывности. Если $x_0\in\mathbb{R}$ - точка непрерывности функции $f(x)$, то, по определению, для любого $n\in\mathbb{N}$ существует такое число $\delta>0$, что для всех $x\in(x_0-\delta,x_0+\delta)$ выполняется неравенство $|f(x)-f(x_0)|<\frac{1}{2n}$. Тогда для любых $x,y\in(x_0-\delta,x_0+\delta)$ получаем

$$|f(x)-f(y)|=|f(x)-f(x_0)+f(x_0)-f(y)|\leqslant$$

$$\leqslant|f(x)-f(x_0)|+|f(y)-f(x_0)|<\frac{1}{2n}+\frac{1}{2n}=\frac{1}{n}$$

,
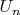
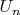
откуда следует, что интервал $(x_0-\delta,x_0+\delta)$ содержится в нашем множестве $U_n$ вместе с точкой непрерывности $x_0$. Так как мы предположили, что функция $f(x)$ непрерывна во всех рациональных точках, отсюда следует, что открытое (как объединение интервалов) множество $U_n$ содержит все рациональные точки и, следовательно, всюду плотно на числовой прямой, а его дополнение $F_n=\mathbb{R}\setminus U_n$ замкнуто и нигде не плотно.

2) Пусть нам задана последовательность нигде не плотных множеств $F_n\subseteq\mathbb{R}$, $n\in\mathbb{N}$. Нужно доказать, что множество иррациональных чисел не содержится в $\bigcup_{n\in\mathbb{N}}F_n$. Напротив, заранее будем предполагать, что множество рациональных чисел содержится в этом объединении. Если это вдруг не так, то перечислим все рациональные числа в виде последовательности $\{r_n:n\in\mathbb{N}\}$ (надеюсь, Вы знаете, как это сделать) и заменим каждое из множеств $F_n$ множеством $F_n\cup\{r_n\}$; при этом все наши множества останутся нигде не плотными.
Так как множество $F_1$ нигде не плотно, существует отрезок $[a_1,b_1]\subseteq\mathbb{R}\setminus F_1$, длина которого удовлетворяет неравенству $0<b_1-a_1\leqslant 1$.
Предположим, что для некоторого $n\in\mathbb{N}$ уже построен отрезок $[a_n,b_n]\subseteq\mathbb{R}\setminus F_n$, длина которого удовлетворяет неравенству $0<b_n-a_n\leqslant\frac{1}{n}$.
Так как множество $F_{n+1}\cap(a_n,b_n)$ нигде не плотно, существует отрезок $[a_{n+1},b_{n+1}]\subseteq[a_n,b_n]\setminus F_{n+1}$, длина которого удовлетворяет неравенству $0<b_{n+1}-a_{n+1}\leqslant\frac{1}{n+1}$, и мы можем продолжать построение неограниченно.
Кроме перечисленных свойств, наше построение обеспечивает выполнение условия
$$[a_1,b_1]\supseteq[a_2,b_2]\supseteq[a_3,b_3]\supseteq\ldots\supseteq[a_n,b_n]\supseteq\ldots$.
По теореме о стягивающейся последовательности отрезков (надеюсь, Вы её помните), существует единственная точка $q_0\in\mathbb{R}$, принадлежащая всем отрезкам $[a_n,b_n]$, $n\in\mathbb{N}$. Точка $q_0$, по построению, не принадлежит $\bigcup_{n\in\mathbb{N}}F_n$ и, в частности, не является рациональным числом.
Таким образом, множество иррациональных чисел не содержится в $\bigcup_{n\in\mathbb{N}}F_n$ и, следовательно, не является множеством первой категории.

[Os]

Так вот читаю но интересно док-во того что множество открыто тогда и только тогда когда дополнительное множество является замкнутым...ламовато но в голове док-ва нет а ето есть задача...

[pokemon]

А как доказать что множество открыто тогда и только тогда когда дополнительное множество является замкнутым

[dm]

По определению открытого и замкнутого множества.

[Гость]

dm писал(а):

По определению открытого и замкнутого множества.

Может ты это всё напишешь... Подробно если не в падлу. ПЛИИИИИИИИИИИИЗ!!!!

[Someone]

Anonymous писал(а):

dm писал(а):

По определению открытого и замкнутого множества.

Может ты это всё напишешь... Подробно если не в падлу. ПЛИИИИИИИИИИИИЗ!!!! :lol: :lol: :lol:

Господи, да что же за вопрос такой!

Главное, ответ зависит от определения открытых и замкнутых множеств.

В рамках общей топологии открытые множества вводятся аксиоматически и, соответственно, никак не определяются, лишь требуется, чтобы открытые множества топологического пространства $X$ удовлетворяли следующим простым аксиомам (символ $\Lambda$ обозначает пустое множество; я так привык; если Вы привыкли к символу $\varnothing$, замените $\Lambda$ на $\varnothing$):

Т1. множества $\Lambda$ и $X$ открыты;
Т2. объединение любого семейства открытых множеств открыто;
Т3. пересечение любого конечного семейства открытых множеств открыто.

После этого замкнутые множества определяются как дополнения открытых.
Поэтому при таком подходе ответ на Ваш вопрос - по определению.

Другая ситуация, если исходным понятием является окрестность точки. Вероятно, Вас интересует в основном случай числовой прямой, где окрестностями точки $x\in\mathbb R$ называют интервалы вида $(x-\delta,x+\delta)$, где $\delta$ - любое положительное число (иногда - просто любые интервалы, содержащие точку $x$, это совершенно эквивалентно). Я дальше всё формулирую для множества действительных чисел, но в произвольном топологическом пространстве тоже можно ввести понятие окрестности точки (например, можно считать окрестностью точки любое открытое множество, содержащее эту точку; можно также ввести окрестности аксиоматически, но я не буду выписывать соответствующие аксиомы, хотя они очень просты).
Для определения открытого множества обычно используется понятие внутренней точки: точка $x\in\mathbb R$ называется внутренней точкой множества $M\subseteq\mathbb R$, если эта точка имеет окрестность, содержащуюся в множестве $M$. Заметим, что внутренняя точка множества автоматически ему принадлежит.
Множество $U\subseteq\mathbb R$ называется открытым, если каждая его точка является внутренней. Определённые таким образом открытые множества удовлетворяют перечисленным выше аксиомам открытых множеств.
Для определения замкнутого множества обычно используется понятие точки прикосновения множества: точка $x\in\mathbb R$ называется точкой прикосновения множества $M\subseteq R$, если каждая окрестность точки $x$ имеет непустое пересечение с множеством $M$.
Множество $F\subseteq\mathbb R$ называется замкнутым, если оно содержит все свои точки прикосновения.

Теперь для доказательства того, что множество $F\subseteq\mathbb R$ замкнуто тогда и толоько тогда, когда его дополнение $U=\mathbb R\setminus F$ открыто, достаточно заметить, что точка $x\in\mathbb R$ является точкой прикосновения множества $F$ тогда и только тогда, когда она не является внутренней точкой множества $U$.

P.S. Почему здесь (именно на этой странице) такие длинные строки? Неудобно читать.

[dm]

Исправлено.

[Dan_Te]

А почему вы пустое множество обозначаете лямбдой? Это какая-то математическая школа?

Вообще-то я хотел спросить, зачем самому пространству быть открытым в определении топологии. Посмотрел КоФо, и там действительно так. Вот только зачем мы вписываем это в аксиомы? Это для лучшей совместимости с другими мат. объектами, типа как "0!=1"?

[dm]

Dan_Te писал(а):

Вообще-то я хотел спросить, зачем самому пространству быть открытым в определении топологии. Посмотрел КоФо, и там действительно так. Вот только зачем мы вписываем это в аксиомы? Это для лучшей совместимости с другими мат. объектами, типа как "0!=1"?

Чтобы антидискретная топология $\{\varnothing,X\}$ была топологией.

[Dan_Te]

Да, точно. А более существенные применения есть? =))