Anonymous писал(а):
Someone писал(а):
Пересечение всех множеств
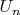
, разумеется, совпадает с множеством точек непрерывности функции

...
А откуда это следует?
Из определения непрерывности функции и определения множеств
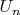
,

.
Прежде всего, как уже
объяснялось, каждое из множеств
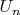
,

, содержит все точки непрерывности функции

, поэтому и

содержит все точки непрерывности функции

. Остаётся только доказать, что функция

непрерывна в каждой точке

.
Но это уже совсем просто. Зададимся произвольным

. Найдётся натуральное число

. Так как

, по определению множества
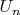
найдётся такой интервал

, что

и

для всех

. Положим

. Тогда

и, следовательно, для всех

(и

) выполняется неравенство

.
Таким образом, мы для произвольного

нашли такое

, что для всех

выполняется неравенство

, а это (по определению) означает непрерывность

в точке

.