Общепринятое обозначение, да,
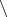
. Но обычный минус тоже иногда встречается, особенно в старых книгах.
А задачи можно разные предлагать. А вообще события - это тоже множества, относительно них же у вас не возникает вопросов.
А во втором примере минусов нет, а его решение будет верно в любой решетке - будь то булева алгебра {0,1}, булева алгебра подмножеств некоторого множества,

-алгебра событий или что-то еще.