задачи по случайным процесам

[Chingizua]

Помогите решить пожалуйста 2 задачки
1)случайный процес омега1=омега(exp^t-1) где омега винеровский процес с зависящими от времени коефициентами сноса а, и дифузией сигма в квадрате. Доказать что омега1 тоже винеровский процес и найти его коефициенты сноса и дифузию

[Someone]

Формулы по-человечкски написать нельзя? Вы имели в виду $\omega_1=\omega(e^t-1)$?

$\omega_1=\omega(e^t-1)$

Первые шаги в наборе формул
Краткий ФАК по тегу [mаth].

[Chingizua]

да именно так а есть просто еще не разобралсякак писать тут формулі

[bubu gaga]

$$ d\omega = a(t) \, dt + \sigma(t) \, dW $$

$$ \omega_1 = \omega \, (e^t - 1) $$

По-моему, такие процессы называются Ито-процессами (но не суть важно). Пользуемся небезызвестной леммой

$$ d\omega_1 = \frac{\partial \omega_1}{\partial t} \, dt + \frac{\partial \omega_1}{\partial \omega} \, d\omega + \frac{1}{2} \, \frac{\partial^2 \omega_1}{\partial \omega^2} \, \sigma_2 \, dt $$

Никакого красивого выражения у меня не получилось, а получилось вот что (требует проверки!)

$$ d\omega_1 = \bigl(\omega(t) \, e^t + e^t \, a(t) - a(t) \bigr) \, dt \; + \; (e^t - 1) \, \sigma(t) \, dW $$

[Chingizua]

спасибо, а как насчет того есть ли процес винеровским?

[bubu gaga]

Как у Вас в конспектах определён Винеровский процесс?

[Chingizua]

как R d-значный процес с независимыми приростами на R+

[bubu gaga]

Формула его общего вида у Вас есть, или нет?

[Chingizua]

нету, есть только что среднее значение меньше бесконечности и условие линбергда.
а откуда берется 'небезызвестная лемма" ?

[bubu gaga]

http://ru.wikipedia.org/wiki/Стохастическое_исчисление_Ито

А какую же тему (если не эту) Вы сейчас изучаете?

[Chingizua]

ну винеровский процес была у нас пара в начале семестра пробежали и все а у меня тут с 10 задач на зачет половину решил а над второй мучаюсь

[bubu gaga]

Но лемму Ито Вы же проходили? Проблем вот в чём

Hull. Options, Futures and Other Derivatives (пятое издание стр. 219) определяет стандартный Винеровский процесс, как процесс без сноса, и дисперсией прямо пропорциональной времени.

$$ \Delta W \approx \epsilon \, \sqrt{\Delta t} $$

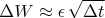
, где $\epsilon \sim N(0, 1)$

Обобщённый винеровский процесс определяется как процесс с постоянной скоростью сноса и постоянной диффузией

$$ dX = \mu \, dt + \sigma \, dW $$

А Ито-процесс определяется таким образом, что снос и диффузия могут зависеть как от состояния $X(t)$, так и от времени $t$.

$$ dX = \mu(X, t) \, dt + \sigma(X, t) \, dW $$

Но если у Вас с самого начала были снос и диффузия, и это называлось Винеровским процессом, то делайте выводы.

[Chingizua]

но ведь в стандартоном винеровском процесе коеф. сноса єто скорость течения в жидкости а дифузия-флуктуация температуры

[bubu gaga]

Таких деталей я не знаю, но коли у Вас Винеровский процесс определили таким образом, значит и $\omega_1$ будет Винеровским. Подождите, может кто из специалистов подойдёт, ответит, я в этих вопросах не то чтобы очень...

[antbez]

Для того чтобы процесс был винеровским, нужно, чтоб у него были непрерывные траектории (очевидно, выполняется для $\Omega_1$) ,независимые приращения (легко проверить) и вероятностное распределение должно зависеть только от приращений. Тут я бы посоветовал для исходного СП выписать вероятностное распределение (там интеграл от экспоненты должен быть) и написать аналогичное распределение для $\Omega_1$