Упражнения потом проверю.
В предыдущих сообщениях Вы привели несколько геометрически наглядных примеров автоморфизмов.
А возможно представить геометрически наглядно изоморфизм?
Если уж Вы так хотите наглядную аналогию, то вообразите - ну, не два трехмерных координатных пространства, это сложно, а просто две плоскости. Вспомните мою аналогию с двумя базисами и берите первый базис в одной плоскости, а второй - в другой. Вот Вам и будет изоморфизм между двумя плоскостями, т.е. между двумерными линейными пространствами.
Но на самом деле в этом нет особой необходимости, потому что разница между авто- и изоморфизмом чисто формальная. И сейчас я объясню, почему.
Строго говоря, разница, конечно, есть. Автоморфизм - это изоморфизм пространства с самим собой. А бывает ведь изоморфизм с другими пространствами. Например, рассмотрим

и

как линейные пространства с естественными операциями сложения и умножения на скаляр. Все скаляры берутся из

, в

сложение покоординатное:
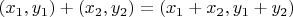
. В пространстве

есть подпространство
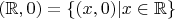
, состоящее из всех пар, второй элемент которых равен нулю. Также как есть подпространство
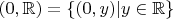
, состоящее из всех пар, первый элемент которых равен нулю.
Упражнение.
1) покажите, что
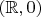
и
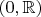
- это подпространства линейного пространства

2) постройте изоморфизм между
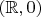
и
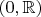
3) постройте изоморфизм между
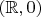
и

, а также между
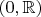
и

.
Так вот. По построению,

, и
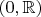
, и
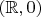
- это три разных множества. Первое состоит из чисел, а второе и третье - из пар чисел. Причем в одном первый элемент пары тождественно равен нулю, а в другом - второй. Но эти линейные пространства изоморфны. А что это значит - изоморфны? Формально только то, что между ними есть линейная биекция. А на самом деле много большее.
Это большее можно выразить простой фразой:
наука о линейных пространствах изучает те и только те свойства, которые сохраняются при их изоморфизме. Пусть есть изоморфизм
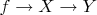
. Размерность пространства

равна

? Значит, размерность

такая же. Выделили некоторое подпространство

размерности

? Его изоморфный образ
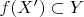
тоже будет подпространством

размерности

. Определили некоторый линейный оператор
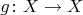
, вычислили его ядро
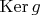
, образ
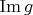
, ранг

? Значит, есть точно такой же линейный оператор
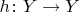
, причем для любого

имеем
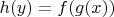
, где

, и ранг

будет тоже

, и
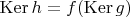
, и
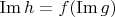
И т.д. и т.п. Все эти факты можно строго доказать (при желании займитесь).
То есть, изоморфные линейные пространства имеют одни и те же "линейно-пространственные" свойства. А не "линейно-пространственные" свойства (например, из чисел оно там состоит, из пар или из чертей в ступах) нам в рамках этой науки не интересны, мы от них отвлекаемся. Так что получается? То, что с точки зрения науки о линейных пространствах изоморфные пространства - это в некотором смысле
одно и то же пространство. Ну как с точки зрения экономики монета в 10 рублей и купюра в 10 рублей - это одинаковое количество денег, а их физические различия экономику не интересуют.
Кстати, этот подход - выделять "главную биекцию" и изучать только те свойства, которые сохраняются при этой биекции - распространяется далеко за пределы теории линейных пространств. Например, у пространств со скалярным произведением (евклидовых, унитарных и других) есть свой изоморфизм, более сложный, чем у линейных пространств. И у аффинных пространств свой. И эти разделы линейной алгебры изучают те свойства, которые сохраняются этими изоморфизмами. Линейной алгеброй дело не ограничивается: например, теория групп изучает свойства, которые сохраняются изоморфизмом групп. Там тоже можно считать, что изоморфные группы - это одна и та же группа. И даже алгеброй дело не огранивается. Например, метрическая геометрия изучает только те свойства, которые сохраняются при изоморфизме метрических пространств, он же изометрия (это биекция, сохраняющая расстояния). В топологии тоже есть свой изоморфизм, он называется гомеоморфизм, и предмет топологии - свойства, которые он сохраняет. Но это уже в сторону разговор, Вам пока рано вдаваться в такие высокие обобщения.
P.S. Вам,
sydorov, на редкость приятно что-то объяснять. Вы понятливы и старательны.