Грубейшим образом линейный оператор можно представить как функцию, аргументом которой являются вектор, "под капотом" он изменяет базис,
возвращает новый вектор, с координатами из старого базиса.
Это Вы описали автоморфизм, а не произвольный линейный оператор. Для произвольного линейного оператора образ базиса - не обязательно базис. Например, оператор, отображающий все векторы в

- линейный (проверьте).
Термин автоморфизм для меня новый.
А термин "изоморфизм"?
Автоморфизм - это просто изоморфизм линейного пространства с самим собой. Автоморфизмом линейного пространства

является любой взаимно-однозначный линейный оператор

(докажите), или, что то же самое, любой линейный оператор

, для которого прообраз нуля - нуль (докажите).
Почему бы нам просто не сказать, что это переход к новому базису в том же пространстве?
Под переходом к новому базису обычно понимается вот что. Дан базис
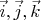
. Вектор

имеет в нем координаты

. Возьмем другой базис
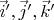
. Вычислить координаты
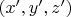
того же самого вектора

в новом базисе. Такая задача часто встречаются на практике, поэтому в учебниках обычно есть раздел "переход к новому базису".
Автоморфизм - это несколько иное. Дан базис
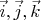
и взаимно-однозначный линейный оператор

. Поскольку этот оператор линейный и взаимно-однозначный, то тройка векторов
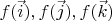
тоже будет базисом, причем таким, что вектор
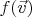
будет иметь в базисе
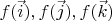
те же координаты

, которые вектор

имеет в базисе
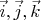
. Этот факт позволяет лучше понять, что такое автоморфизм. Но на практике обычно нужно вычислить координаты вектора
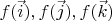
в "старом" базисе
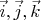
, а не в новом. Эти координаты зависят от конкретного автоморфизма. Они будут разными для, например, четырех следующих автоморфизмов:
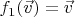
(тождественный автоморфизм),
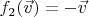
(отражение относительно начала координат),
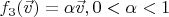
(сжатие),
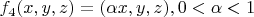
(сжатие по одному измерению).
Чтобы понять разницу между сменой базиса и автоморфизмом, выполните следующие упражнения.
Дан базис
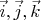
. Вектор

имеет в нем координаты

. Для каждого из четырех перечисленных операторов найдите:
1) базис
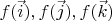
;
2) координаты вектора

в базисе
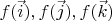
;
3) координаты вектора
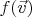
в базисе
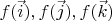
.