Скорость гравитации

[Mikhail_K]

realeugene в сообщении #1708418 писал(а):

Сила - ковариантный вектор

Почему?

[realeugene]

Mikhail_K в сообщении #1708422 писал(а):

Почему?

Хотя бы потому, что интеграл трёхмерной силы по перемещению даёт трёхмерный скаляр - работу силы.

Да и если у нас летит вбок горизонтальный квадрат с натянутой по диагонали ниткой, то ширина квадрата в неподвижной ИСО становится меньше высоты, а пересчитанная через преобразование Лоренца 4-силы горизонтальная компонента 3-силы натяжения летящей нитки оказывается больше вертикальной.

[Cos(x-pi/2)]

realeugene в сообщении #1708357 писал(а):

Мне же всё-таки интересны ещё и способы интуитивных рассуждений, дающие при этом правильный, хоть и заранее известный результат.
<...>

Ни от каких других точек траектории космонавта мы в нашей мелкой локальной области свет наблюдать не можем - он или ещё к нам не прилетел, или уже мимо нас улетел дальше. Так что мы видим, что свет фонарика космонавта приходит к нам сзади, где космонавт был когда-то.

Почему бы тогда не применить аналогичную интуитивную "аргументацию" для поля равномерно прямолинейно движущегося заряда - пусть бы оно указывало туда, где космонавт был когда-то :) Кстати, вклад в поле от ускорения заряда, если оно не равно нулю, как раз такой - запаздывающий.

(Просто, по своему опыту могу утверждать, что большинство задач в "не школьной" физике интуитивно не решаются. Интуиция нередко обманывает. Или бывает и так, что решаются, но интуитивные рассуждения при этом оказываются очень запутанными и не убедительными. Бывает также, что заранее известный результат люди "выводят" неверными рассуждениями (а будь результат неизвестным, они его и не вывели бы никогда из такой интуиции).

Поэтому считаю очень сомнительной ценность итуитивной аргументации в неочевидных задачах. Формализм для того и был изобретён, чтобы не усложнять (и не чтобы выгонять с экзамена, как думают некоторые студенты), а упрощать нахождение решений. После того, как решение той или иной задачи выведено регулярным методом, можно, конечно, пытаться подыскать для него интуитивно понятную интерпретацию (но не факт, что она обязательно найдётся) - чтобы она послужила дополнительным способом запоминания результата.)

[realeugene]

Cos(x-pi/2) в сообщении #1708429 писал(а):

Почему бы тогда не применить аналогичную интуитивную "аргументацию" для поля равномерно прямолинейно движущегося заряда - пусть бы оно указывало туда, где космонавт был когда-то

Потому что на нулевой частоте нет распространяющейся со скоростью света волны.

Cos(x-pi/2) в сообщении #1708429 писал(а):

Интуиция нередко обманывает.

Когда интуиция обманывает - это самое интересное. Референсное решение всё равно даётся точным расчётом, безусловно.

Cos(x-pi/2) в сообщении #1708429 писал(а):

После того, как решение той или иной задачи выведено регулярным методом, можно, конечно, пытаться подыскать для него интуитивно понятную интерпретацию (но не факт, что она обязательно найдётся) - чтобы она послужила дополнительным способом запоминания результата.)

И я об этом. В рассматриваемом случае летящего с постоянной скоростью заряда точное решение давно посчитано до нас.

[Cos(x-pi/2)]

realeugene в сообщении #1708434 писал(а):

Потому что на нулевой частоте нет распространяющейся со скоростью света волны.

Вы это из интуитивных соображений вывели? Если да, то согласно такой вашей аргументации вот в той же мере обоснованный ответ на исходный вопрос: раз на нулевой частоте запаздывающей волны нет, а поле, тем не менее, нулю не равно, то оно обязательно направлено из точки мгновенного положения заряда (или в эту точку, если заряд отрицательный), - потому что больше некуда ему быть направленным.

[realeugene]

realeugene в сообщении #1708415 писал(а):

Наклонная летящая ниточка тянет вбок?

Кстати, любопытный контринтуитивный результат. Когда в ракете пролетает с постоянной скоростью мимо в кулоновском поле неподвижного заряда привязанный на нитке пробный заряд, в ИСО неподвижного заряда нитка с пробным зарядом не направлена на неподвижный заряд почти нигде.

-- 06.11.2025, 23:23 --

Cos(x-pi/2) в сообщении #1708437 писал(а):

Если да, то согласно такой вашей аргументации вот в той же мере обоснованный ответ на исходный вопрос: раз на нулевой частоте запаздывающей волны нет, а поле, тем не менее, нулю не равно, то оно обязательно направлено из точки мгновенного положения заряда (или в эту точку, если заряд отрицательный), - потому что больше некуда ему быть направленным.

Интересный аргумент. Нужно подумать, какие у него подводные камни. Например, поле может оказаться направлено в точку, только пропорциональную мгновенному положению летящего заряда. Так что всё-таки в решении должно быть важно, что при преобразовании Лоренца статического поля поперечные компоненты умножаются на гамма-фактор, а продольная компонента напряжённости не изменяется. Это должно компенсировать сжатие продольных длин в ракете. Но в этом месте моя интуиция всё ещё ломается.

Да, на нулевой частоте нет дальнего поля, как и волн. Так что брать предел волновых решений к нулевой частоте некорректно, по крайней мере в электродинамике Максвелла.

[Cos(x-pi/2)]

realeugene в сообщении #1708438 писал(а):

Кстати, любопытный контринтуитивный результат. Когда в ракете пролетает с постоянной скоростью мимо в кулоновском поле неподвижного заряда привязанный на нитке пробный заряд, в ИСО неподвижного заряда нитка с пробным зарядом не направлена на неподвижный заряд почти нигде.

Ничего контринтуитивного тут нет; движение заряженного тела на нитке в поле движущегося заряда это вообще совсем другая задача. Пробное заряженное (зарядом $q_1)$ тело на нитке имеет не равную нулю массу $m.$ Внешнее поле действует на него с силой $q_1\mathbf{E}+q_1[(\mathbf{v}/c)\times\mathbf{H}].$ Этой силой плюс силой натяжения нити определяется только ускорение пробного тела, а какая у него будет в каждый момент времени скорость $\mathbf{v}(t)$ и радиус-вектор $\mathbf{r}(t),$ - это зависит ещё и от начальных скорости $\mathbf{v}(t_0)$ и положения $\mathbf{r}(t_0).$ Т.е. чтобы найти траекторию $\mathbf{r}(t),$ надо интегрировать уравнение движения пробного тела с конкретными заданными начальными условиями. Нет универсального ответа для $\mathbf{r}(t),$ не зависящего от начальных условий.

Исходная задача - о направлении электрического поля - намного проще, чем механика тела на нитке. На мой взгляд, нет смысла усложнять задачу телами с нитками, если речь идёт о решении исходной простой задачи о направлении поля.

[realeugene]

Cos(x-pi/2) в сообщении #1708439 писал(а):

Исходная задача - о направлении электрического поля - намного проще, чем механика тела на нитке.

Я специально переформулировал задачу про движение пробного заряда на нитке в стационарном кулоновском поле, чтобы избавиться от магнитного поля. И от сложной динамики можно избавиться стандартным образом: устремив массу пробного заряда к нулю, введя небольшое демпфирование, чтобы погасить колебания. Тогда в каждый момент времени направление нитки (короткой) определяется квазистатическим равновесием действующих на заряд в этот момент сил.

[realeugene]

realeugene в сообщении #1708438 писал(а):

Так что всё-таки в решении должно быть важно, что при преобразовании Лоренца статического поля поперечные компоненты умножаются на гамма-фактор, а продольная компонента напряжённости не изменяется. Это должно компенсировать сжатие продольных длин в ракете. Но в этом месте моя интуиция всё ещё ломается.

Прокачал интуицию.

Выше подсмотрены формулы преобразования от статического кулоновского поля в ИСО заряда к полю летящего в направлении $Ox$ заряда в нашей неподвижной ИСО. Выше были подсмотрены формулы преобразования $E_x = E'_x$, $E_y = \gamma E'_y$, где штрихованые координаты относятся к летящей ИСО заряда.

Преобразование поля нужно делать для одного и того же события в разных ИСО. Пусть в $t=0$ заряд пролетает через начало координат неподвижной ИСО. При рассмотрении одновременных событий в неподвижной ИСО (при $t=0$) горизонтальные расстояния из ИСО летящего заряда сжались. Т. е. событие с пространственными координатами $(x, y)$ в неподвижной ИСО (и нулевым временем в ней) имеет координаты $(x', y') = (\gamma x, y)$ в ИСО летящего заряда в какой-то ненулевой вообще говоря момент времени там. Так как там поле стационарно, то штрихованное время нам не интересно. А так как электрическое поле там радиально, имеем $E'_x/E'_y=x'/y'=\gamma x/y$. Подставляем в подсмотренные формулы преобразования: $E_x/E_y=\left(1/\gamma\right) E'_x/E'_y = x/y$. То есть электрическое поле в неподвижной ИСО на самом деле направлено в центр координат радиально в тот момент в этой ИСО, когда через начало координат пролетает создающий поле заряд, а значит, ввиду произвольности выбора начала координат, оно всегда направлено в направлении текущего положения равномерно летящего создающего поле заряда.

Любопытно, что хотя $E_y$ в $\gamma$ раз больше, чем $E'_y$, но на летящий рядом с той же скоростью пробный заряд воздействует в неподвижной ИСО за счёт дополнительного магнитного поля вертикальная сила Лоренца в $\gamma$ раз меньше, чем в штрихованных координатах. Это согласуется с общим правилом: при переходе из движущихся координат к неподвижным, у прилагаемых к неподвижным в движущихся координатах точках сил поперечные компоненты ослабляются в $\gamma$ раз, а продольная компонента сохраняется.

[Cos(x-pi/2)]

realeugene в сообщении #1708440 писал(а):

Я специально переформулировал задачу про движение пробного заряда на нитке в стационарном кулоновском поле, чтобы избавиться от магнитного поля.

Мне непонятно, нафига это Вам надо. Неподвижный заряд-источник поля (т.е. в ИСО-1) не создаёт магнитного поля. Движущийся заряд-источник поля (т.е. тот же заряд, рассматриваемый в ИСО-2) магнитное поле создаёт обязательно; но это магнитное поле можно просто-напросто не рассматривать. Потому что на неподвижный заряд-детектор оно не действует; а заряд-детектор на предельно короткой ниточке, с длиной стремящейся к нулю, вслед за движением заряда-источника будет поворачиваться с линейной скоростью, стремящейся к нулю (при подходящем выборе начальных условий), так что магнитной силой Лоренца можно пренебречь, и все дела.

realeugene в сообщении #1708438 писал(а):

Так что всё-таки в решении должно быть важно, что при преобразовании Лоренца статического поля поперечные компоненты умножаются на гамма-фактор, а продольная компонента напряжённости не изменяется. Это должно компенсировать сжатие продольных длин в ракете. Но в этом месте моя интуиция всё ещё ломается.

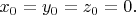
Да чего ей ломаться-то, если у Вас уже идут в дело преобразования Лоренца. В ИСО-1 (пользуюсь своими обозначениями из этого сообщения, штрихованные величины будут относиться к ИСО-2, а в ИСО-1 они у меня все нештрихованные) заряд-источник поля неподвижен, он всё время находится в начале координат $x_0=y_0=z_0=0.$ Его поле в произвольной точке $x,y,z,$ отличной от начала координат, есть:

$$E_x=\frac{q}{r^3}x\,,\qquad E_y=\frac{q}{r^3}y\,,\qquad E_z=\frac{q}{r^3}z\,,$$

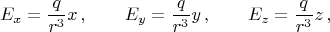
где $r=\sqrt{x^2+y^2+z^2}\,.$

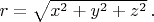
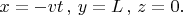
При этом наблюдатель движется по траектории $x=-vt\,,\, y=L\,, \, z=0.$ Значит, поле в точке расположения наблюдателя в каждый момент времени $t$ есть:

$$E_x=\frac{q}{r^3}(-vt)\,,\qquad E_y=\frac{q}{r^3}L\,,\qquad E_z=0\,.$$

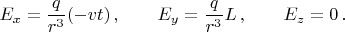
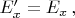
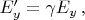
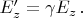
В ИСО-2 преобразования Лоренца для поля дают: $E'_x=E_x\,,$ $E'_y=\gamma E_y\,,$ $E'_z=\gamma E_z\,.$ Значит, поле в точке расположения наблюдателя в каждый момент времени есть:

$$E'_x=\frac{q}{r^3}(-vt)\,,\qquad E'_y=\frac{q}{r^3}\gamma\,L\,,\qquad E'_z=0\,.$$

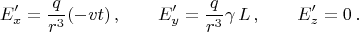
Преобразования Лоренца для координат и времени любого события:

$$ct'=\gamma(ct+\beta x)\,,\qquad x'=\gamma(x+vt)\,,\qquad y'=y\,,\qquad z'=z\,.$$

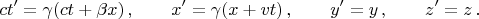
Траектория заряда-источника в этой ИСО-2 это движущаяся по х-оси точка; её координаты:

$$x'_0=vt'\,,\qquad y'_0=0\,,\qquad z'_0=0\,.$$

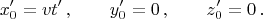
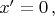
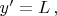
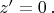
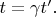
Траектория наблюдателя в этой ИСО-2 это неподвижная точка $x'=0\,,$ $y'=L\,,$ $z'=0\,.$ В ней получается $t=\gamma t'.$ Т.е. здесь есть "эффект замедления времени": $t'$ это интервал собственного времени наблюдателя (время в его системе покоя, ИСО-2), а $t>t'$ это соответствующий ему интервал времени по часам ИСО-1, относительно которой наблюдатель движется. 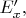Подставив выраженное так $t$ через $t'$ в $E'_x,$ имеем в точке наблюдения поля неподвижным наблюдателем:

$$E'_x=\frac{q}{r^3}\gamma \,(-vt')\,,\qquad E'_y=\frac{q}{r^3}\gamma\,L\,,\qquad E'_z=0\,.$$

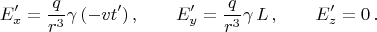
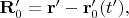
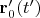
Сравнивая это с компонентами вектора $\mathbf{R}'_0=\mathbf{r}'-\mathbf{r}'_0(t'),$ проведённого в неподвижную точку наблюдения $\mathbf{r}'$ из движущегося по траектории $\mathbf{r}'_0(t')$ заряда-источника:

$$R'_{0x}=0-vt'\,,\qquad R'_{0y}=L-0\,,\qquad R'_{0z}=0-0\,,$$

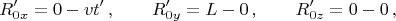
видим, что

$$\mathbf{E}'=\frac{q}{r^3}\gamma \,\mathbf{R}'_0\,.$$

Вот и всё; можете переводить себе это на язык интуиции - с лоренцевским "сокращением длин" и "замедлением времени" (о нём ваша интуиция по-видимому забыла, когда сломалась :)

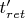
Ещё интересный сюжет - посмотреть, как тот же результат получается из вычислений по потенциалам Лиенара - Вихерта. Там все поля в ИСО-2 поначалу выражаются только через величины в запаздывающие моменты времени $t'_{ret}$. А в итоге результат удаётся переписать в указанном выше виде, т.е. без запаздывания.

[realeugene]

А можно проще. Запаздывания быть не может - поле спереди и сзади симметрично. Рассмотрим прямую, проходящую через центр неподвижной ИСО. Она отображается в проходящую через начало координат прямую в ИСО летящего заряда, пусть и проходящую под другими углами. В точках этой прямой электрическое поле в неподвижной ИСО получается одним и тем же линейным преобразованием поля в соответствующих точках прямой в ИСО летящего заряда. В летящей ИСО все проекции напряжённостей поля подобны и обратны квадратам радиуса. Значит, в точках неподвижной прямой все напряжённости подобны и обратны квадрату расстояния от центра. Но куда они направлены мы не знаем.

Рассмотрим симметричное под некоторым углом вперёд-назад коническое сечение, ограниченное сферами некоторого разного радиуса. Ввиду того, что напряжённости на каждом луче одинаково направлены и обратны квадратам радиуса, электрические потоки через эти сферические заглушки равны. А значит, ввиду теоремы Гаусса, равен нулю суммарный поток через образованные прямыми боковые стенки конусов. А значит, ввиду симметрии, напряжённости электрического поля там направлены вдоль этих образующих. То есть, по радиусу в центр к мгновенному положению летящего заряда.

-- 07.11.2025, 02:51 --

Cos(x-pi/2) в сообщении #1708442 писал(а):

а заряд-детектор на предельно короткой ниточке, с длиной стремящейся к нулю, вслед за движением заряда-источника будет поворачивается с линейной скоростью

Вот только эта ниточка будет направлена на источник. А сила Лоренца - нет.

Если заряд неподвижен, и летит мимо с практически постоянной скоростью тестовый заряд на ниточке, то ниточка в ИСО источника не направлена на источник, хоть сила Лоренца в ИСО неподвижного заряда и направлена.

[wrest]

Видно, что тема "зашла". С движением по инерции (прямолниейно-равномерным) понятно.
Усложним вопрос.
Теперь мимо покоящихся нас пролетает массивный (но не чрезмерно, т.е. поля "слабые") светящийся электрический заряд, причем летит относительно покоящихся нас прямолинейно-равноускоренно.
Причем в этом режиме (прямолинейно-равноускоренном) он летит как минимум с того момента (по нашим часам), как был излучен свет, который покоящиеся мы регистрируем по нашим часам сейчас.

Куда будут показывать наши датчики направления электрического поля ("электростатический компас") и гравитационного по отношению к "видимому" положению летящего заряда т.е. к направлению падающего на нас видимого света.
Т.е. куда покоящихся нас будет притягивать массивный электрический заряд гравитационно и электростатически -- в одно направление или разные, и в какие.

[realeugene]

wrest в сообщении #1708471 писал(а):

Причем в этом режиме (прямолинейно-равноускоренном)

Постоянно собственное ускорение?

По поводу электрического поля нужно считать. Симметрия по обращению времени разрушена. В случае гравитационного поля может оказаться, что задача сильно сложнее и недоопределена: чтобы ускорять летящий заряд ему нужно снаружи передавать порток энергии-импульса, и этот поток сам должен как-то гравитировать. На электрическое поле внешние потоки энергии-импульса не влияют.

Постоянное ускорение - это тоже нулевая частота, так что волновые решения тоже некорректно экстраполировать и тут. Особенность задачи ещё и в том, что нет ИСО, в которой поле заряда кулоновское. Так что игры с преобразованиями Лоренца не помогут. Пока вижу один путь: через потенциалы Льенара-Вихерта. Должно быть не сложно.

[epros]

realeugene в сообщении #1708424 писал(а):

Mikhail_K в сообщении #1708422 писал(а):

realeugene в сообщении #1708418 писал(а):

Сила - ковариантный вектор

Почему?

Хотя бы потому, что интеграл трёхмерной силы по перемещению даёт трёхмерный скаляр - работу силы.

А откуда Вы взяли, что в этом интеграле не должно быть метрического тензора?

Импульс, по крайней мере, удобнее понимать как три координаты контравариантного четырёхвектора. Но вообще-то можно по-разному определять.

[realeugene]

epros в сообщении #1708476 писал(а):

А откуда Вы взяли, что в этом интеграле не должно быть метрического тензора?

epros в сообщении #1708476 писал(а):

Импульс, по крайней мере, удобнее понимать как три координаты контравариантного четырёхвектора

В четырехмерном случае всё немного иначе, конечно. Там и энергия больше не скаляр. Но если есть метрический тензор (трёхмерный) - это просто опускание индексов чтобы получить форму, которую интегрируют.

В общем, смотреть можно с разных сторон и это всё не принципиально, но стоит помнить, что 3-сила преобразуется преобразованиями Лоренца совсем не так, как пространственные координаты. В результате, на самом деле, летящая под углом натянутая нитка тянет не вдоль себя.