Канонические формы уравнений n-й степени

[Утундрий]

Пока тема не рухнула в Бездну проективных прямых и прочей алгебраической геометрии, призову, пожалуй, Тени Предков.

Начнём с кубики. Сдвигом и растяжением приведём уравнение к следующей форме:

$$\boxed{z^3=2+3pz, \quad p\ne 0} \eqno (z^3, 1)$$

Как завещали Сципион дель Ферро и Тарталья, сделаем подстановку

$$\boxed{z=a+b} \eqno (z^3,2)$$

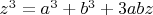
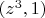
Тогда $z^3=a^3+b^3+3abz$ и мы запросто удовлетворим $(z^3, 1)$ внаглую потребовав

$$\left\{ {\begin{array}{l} a^3+b^3=2 \\ ab=p \\ \end{array} } \right. \eqno (z^3,3)$$

Поскольку соотношения пахнут Вьетом, составим комбинацию
$(w-a^3)(w-b^3)=w^2-2w+p^3=(w-1)^2+p^3-1$
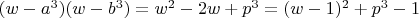
Приравнивая это нулю и решая квадратное уравнение, находим

$$\left\{ {\begin{array}{l} a= \root 3 \of {1+\sqrt{1-p^3}}\\ b= \root 3 \of {1-\sqrt{1-p^3}}\\ ab=p \\ \end{array} } \right. \eqno (z^3,4)$$

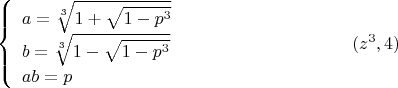
Собственно, ради такой красоты и подбирались коэффициенты в $(z^3, 1)$.

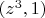
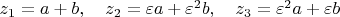
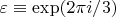
Искомые корни суть $z_1=a+b, \quad z_2=\varepsilon a+\varepsilon^2 b, \quad z_3=\varepsilon^2 a+\varepsilon b$, где $\varepsilon \equiv \exp (2\pi i /3)$. Или, в явном виде

$$a+b, \quad - \frac {a+b}{2} \pm i \frac {a-b}{2} \sqrt 3 \eqno (z^3,5)$$

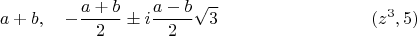
Возьмём теперь квартику и сдвигом и растяжением приведём к виду:

$$\boxed{z^4=3+4pz+6qz^2, \quad |p|+|q|\ne 0} \eqno (z^4, 1)$$

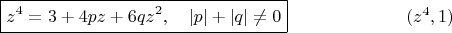
По наущению Феррари попытаемся добиться следующего

$$\boxed{(z^2+w-q)^2=(\text{нечто})^2} \eqno (z^4,2)$$

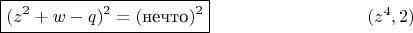
Раскроем слева
$(z^2+w-q)^2=2\left(\sqrt{w+2q}\;z+\dfrac{p}{\sqrt{w+2q}}\right)^2+3+(w-q)^2-\dfrac{2p^2}{w+2q}$
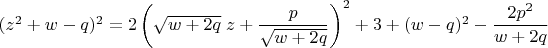
и отбросим хвост справа, что даст следующее уравнение:

$$w^3=2(p^2-3q-q^3)+3(q^2-1)w \eqno (z^4,3)$$

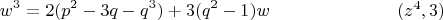
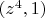
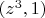
Ради этой двойки с тройкой и подбирались коэффициенты в $(z^4, 1)$. Простым растяжением эта форма (когда это необходимо) сводится к $(z^3, 1)$ с параметром

$$\tilde p=\dfrac {q^2-1}{(p^2-3q-q^3)^{2/3}}$$

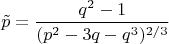
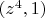
Найдя любое его решение, для отыскания корней $(z^4, 1)$ получим два квадратных уравнения.

$$z^2+w-q \pm \sqrt{2} \left(\sqrt{w+2q}\;z+\dfrac{p}{\sqrt{w+2q}}\right)=0 \eqno (z^4,4)$$

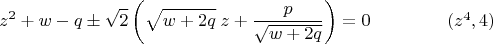
Это простейший, по моему разумению, способ быстро восстановить в памяти обе рассмотренные методики. Правда для этого всё-таки придётся заучить взятые в рамку формулы. Ну или тягать $4$ и $27$ в знаменателях всю дорогу.

[nnosipov]

Утундрий в сообщении #1700258 писал(а):

Возьмём теперь квадрику

Квартику, квадрика это 2-я степень.

Примеров не хватает. Решите по этой методике уравнение $x^4-4x-6=0$.

[Утундрий]

nnosipov в сообщении #1700263 писал(а):

Квартику

Поправил.

nnosipov в сообщении #1700263 писал(а):

Решите по этой методике уравнение $x^4-4x-6=0$.

Мат-пакетами я отнюдь не пренебрегаю. И вид корней предложенного уравнения не внушает большого желания находить их вручную.

[nnosipov]

Утундрий в сообщении #1700265 писал(а):

И вид корней предложенного уравнения не внушает большого желания находить их вручную.

Так здесь корни как раз выглядят не самым забористым образом (но, правда, и не самым простым), и Maple выдает их в более-менее разумном виде, близком к каноническому. Вот и интересно, в каком виде эти корни получатся по Вашей методике.

Кстати, а Вы хоть одно уравнение 4-й степени голыми руками решили?

[Утундрий]

nnosipov в сообщении #1700280 писал(а):

по Вашей методике.

Я, вроде бы сослался на авторов

[nnosipov]

Утундрий в сообщении #1700286 писал(а):

Я, вроде бы сослался на авторов

А у Вас только дизайн что ли? Напоминает классику https://yandex.ru/video/preview/16671910442816545741

[Утундрий]

У меня это не открывается. Так что, если там был не слишком шахтёрский и более-менее уместный юмор, то перескажите своими словами, пожалуйста.

Кстати, к вопросу о кратных корнях. Достаточно очевидно как получить соотношение на параметры, указу́ющие на оные. (Это я так неуклюже пытаюсь привлечь заинтересованную мо́лодеж к обсуждению).

[nnosipov]

Утундрий в сообщении #1700355 писал(а):

У меня это не открывается.

https://www.youtube.com/watch?v=hj-eq6WYThE

[Утундрий]

(Оффтоп)

Я ничего не понял, но мне всё стало ясно (с)

[Утундрий]

Кстати, о мат-пакетах. Вот, например, даже урезанный онлайн-вольфрам и то лихо выдаёт нечто эдакое:

[Утундрий]

Дальше я планирую продвигаться посредством преобразования Чирнгауза. Если кто имел с ним дело на практике, прошу высказаться. Или вдруг есть альтернативные идеи? (Заброс dgwuqtj относительно преобразований Мёбиуса я повертел и пришёл к выводу, что как-то оно неоправданно громоздко получается).