Канонические формы уравнений n-й степени

[Евгений Машеров]

Сдвиг и растяжение - это две степени свободы. Позволяющие избавиться от двух коэффициентов из четырёх для кубического и из трёх для четвёртой степени. То есть у кубического уравнения, когда мы, как обычно, делаем коэффициент при старшей единичным, а при следующей - нулём, остаётся два, а для четвёртой степени - три параметра.
$z^3+pz+q=0$
$z^4+pz^2+qz+r=0$
Приведение к "однопараметрическому виду" возможно лишь для очень специального вида.

[amon]

Утундрий в сообщении #1699988 писал(а):

Сдвигом и растяжением это всегда можно сделать.

Я, видимо, чего-то глубоко не понимаю. Как сдвигом и растяжением привести уравнение $x^2=0$ к виду $z^2=1$?

[dgwuqtj]

amon в сообщении #1700044 писал(а):

Я, видимо, чего-то глубоко не понимаю.

Там скорее разрешается ещё домножать уравнение на константу, все три параметра комплексные и уравнение общего вида (в т.ч. дискриминант ненулевой).

[amon]

То есть, предполагается, что у исходного уравнения все корни разные?

[Утундрий]

Предполагается, что $a_0 a_n \ne 0$.

[Утундрий]

Проще говоря, меня интересует сугубо практический аспект. То есть, предполагается, что я применил все известные мне фокусы-покусы, умею извлекать корни в комплексной области, выделять и отбрасывать нулевые решения, отличаю $x^{39}=p\; x^{13}+q$ от "истинного" уравнения тридцать девятой степени и всё такое.

[nnosipov]

А кратные корни Вы умеете выделять?

[Евгений Машеров]

"С сугубо практической точки зрения" хватает численного расчёта. А общие выводы о поведении корней знания их значения не требуют.
Ну и если не нравится формула Кардано - решайте по Виету, оно как-то понятнее выглядит...

[nnosipov]

Евгений Машеров в сообщении #1700001 писал(а):

Приведение к "однопараметрическому виду" возможно лишь для очень специального вида.

Вот, например, есть уравнение $z^3+pz+q=0$ и $q \neq 0$. Тогда можно считать, что $q=1$ (или любому другому конкретному ненулевому числу). Ведь можно положить $z=q^{1/3}Z$ и после сокращения на $q$ получить уравнение $Z^3+PZ+1=0$, где $P=pq^{-2/3}$.

[Утундрий]

nnosipov в сообщении #1700127 писал(а):

А кратные корни Вы умеете выделять?

Умею. Для этого нужно вычислить дискриминант. То есть результант уравнения и его производной. Или имелось в виду что-то другое?

Евгений Машеров
Да, это в духе времени: засунуть уравнение в мат-пакет и пусть он сам мучается. Только немножко неприятно будет дальше жить с осознанием того прискорбного факта, что без железяки не владеешь математикой шестнадцатого века

[nnosipov]

Утундрий в сообщении #1700143 писал(а):

Только чем мне это здесь поможет, учитывая заявленную тему?

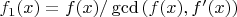
Если многочлен $f(x)$ имеет кратные корни, то многочлен $f_1(x)=f(x)/\gcd{(f(x),f'(x))}$ имеет те же корни, что и $f(x)$, но они у него все уже однократные. При этом степень $f_1(x)$ меньше, вообще говоря, чем степень $f(x)$. Конечно, если априори многочлен $f(x)$ взаимно прост со своей производной (например, он неприводим над каким-то полем), то это ничего не даст, но в общем случае будет выигрыш.

-- Сб авг 30, 2025 13:44:33 --

Утундрий в сообщении #1700143 писал(а):

Да, это в духе времени: засунуть уравнение в мат-пакет и пусть он сам мучается.

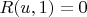
Так иногда по-другому и не получится. Вот в этой теме https://dxdy.ru/topic161336.html есть многочлен $R(u,v)$ (он возник в процессе выяснения вопроса о существовании первого интеграла для довольно небольшой нелинейной системы ОДУ). И вот этот $R(u,v)$ такой, какой есть. Если зафиксировать $v=1$, то Maple вполне шустро (за несколько секунд) находит корни уравнения $R(u,1)=0$ с 1000 знаками (при этом невязка имеет порядок $10^{-850}$). 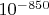Конечно, возникает вопрос, а можно ли доверять таким вычислениям. Я бы доверял, все-таки методы приближенного решения уравнений с одним неизвестным разработаны довольно неплохо (меня так учили). Не понятно, что здесь еще можно изобрести, когда речь идет о нахождении корней многочлена с конкретными числовыми коэффициентами (впрочем, сейчас вспомнил про работы Виктора Пана, люди здесь еще что-то изобретают). Другое дело, когда коэффициенты многочлена зависят от каких-то параметров, но здесь все зависит от постановки задачи, под задачу нужно и метод подбирать. Без конкретики все это досужие разговоры.

[Утундрий]

Отмечу, что отредактировал своё сообщение до того как на него был получен ответ...

Что касается проверки корней. Если бы меня это сильно заботило, то я бы смотрел не на невязку, малость которой мало что доказывает, а скорее в сторону оценок неких контурных интегралов.

[amon]

Утундрий в сообщении #1700104 писал(а):

Предполагается, что $a_0 a_n \ne 0$.

Какой-то велосипед изобретаем. Про второй порядок. Если корни разные, можно один нулевой, то уравнение второго порядка сведется к $z^2=1,$ если одинаковые, то к $z^2=0.$ Тогда уравнение третьего порядка можно свести к однопараметрическому, а 4-го - к двухпараметрическому. Вид уравнения - по желанию, видимо, можно и такой, как у Вас.

[Утундрий]

amon в сообщении #1700218 писал(а):

Вид уравнения - по желанию

Так о том же и тема У кого какие желания? Когда вообще уместен некий специфический вид и как этот вид выглядит?

[dgwuqtj]

Можно вообще разрешить дробно-линейные преобразования и сводить кубическое уравнение к виду $x^3 = 1$.