Поскольку ТС в этой теме сослался на "соседнюю" тему, в которой поначалу он и выдвинул свои возражения против модели бесконечно длинного соленоида, то добавлю пояснения к
тому сюжету. (В той теме основная линия сюжета - качественные выводы о неприменимости в определённых ситуациях понятия "напряжение между точками A и В", с подтверждением в конкретном эксперименте с числовыми результатами измерений осциллографом и с их предварительной оценкой по формулам поля бесконечно длинного соленоида; речь о статье R.H. Romer, Am. J. Phys. 50, 1089 (1982)).
Автор статьи указал значения параметров:

- частота переменного тока

в соленоиде; форма

- пилообразная, так что форма импульса примерно треугольная.

в двух частях треугольного импульса.

- длина соленоида.

- радиус соленоида.

число витков. Так что,

витков на метр.
Автор статьи отмечает, что речь в его опыте идёт об индукционных э.д.с. вблизи середины соленоида.
Если мы обозначим как

"пиковое" значение э.д.с. (примерно прямоугольной формы) в одновитковом контуре вокруг соленоида, и обозначим как
 размах
размах сигнала (автор называет его peak-to-peak voltage), наблюдаемого осциллографом на сопротивлении

в контуре, образованном двумя сопротивлениями, то для этой величины увидим в статье предваряющее опыт предсказание автора, сделанное, как он пишет, по указанным параметрам опыта:

Подробный подсчёт чисел для этой оценки автор в статье не написал, но такой подсчёт элементарно воспроизводится (поэтому и опущен в статье). Для ясности выписываю такой расчёт здесь.
Первый шаг - убедимся в применимости квазистационарного приближения. Основной гармонике с частотой

соответствует длина ЭМ-волны

Треугольный периодический сигнал формально можно представить суммой бесконечного множества нечётных гармоник с амплитудами, убывающими обратно пропорционально квадрату номера гармоники. Но на практике сумма уже всего нескольких гармоник, допустим с номерами

выглядит почти как треугольный сигнал. Т.е., приняв, что на практике максимальная частота гармоники в десять, ну или даже пусть в сто раз больше основной
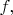
получим для самой маленькой длины волны оценку

или

Это намного больше размеров соленоида в опыте Ромера, в том числе больше и длины провода в соленоиде (она порядка сотен метров).
Таким образом, в данном опыте амплитудное значение магнитного поля

внутри соленоида и вокруг соленоида можно оценивать по формулам магнитостатики - займёмся теперь этим (а об ЭМ-поправках к магнитному полю, связанных с "высокочастотностью", можно уже не думать).
Точные формулы статического поля соленоида конечных размеров есть в литературе, но они очень громоздкие. Учтём упрощающее обстоятельство: в опыте Ромера соленоид длинный - отношение его радиуса к длине есть малая величина

Для длинного соленоида известна из литературы оценка (см., например, Am. J. Phys. 69, 751 (2001) J.Farley, R.H. Price; doi: 10.1119/1.1362694) отношения поля

снаружи вблизи соленоида к полю внутри соленоида с круглым сечением

всё около его середины:

В такой оценке поле

с удалением от соленоида (в плоскости его середины) поначалу не изменяется. Но затем, с дальнейшим увеличением расстояния начинает убывать, и в итоге на больших расстояниях, - там, где соленоид выглядит похожим на магнитный диполь, - поле убывает обратно пропорционально кубу расстояния. (В упомянутой выше статье 2001 года всё это иллюстрируется ещё и на графиках по численному расчёту зависимости поля от расстояния для соленоидов с разной формой поперечного сечения.)
Для рассматриваемого опыта указанная формула даёт:

Т.е. поле снаружи соленоида - мал
о: вблизи соленоида оно составляет всего

% от поля внутри соленоида. Значит, магнитный поток снаружи соленоида через площадь порядка площади сечения соленоида составляет не более

% от магнитного потока внутри соленоида (он направлен в противоположную сторону). Через площадь в

раз большую площади соленоида получится не более

% от от магнитного потока внутри соленоида.
Индукционная э.д.с. в контуре, тесно охватывающем соленоид, практически не зависит от

она определяется скоростью изменения магнитного потока внутри соленоида, который оценивается как

Поэтому, ограничиваясь в опыте разумными условиями с точки зрения любого разумного экспериментатора, - не слишком большими площадями контуров, их достаточной близостью к соленоиду около его середины, и не идеальной точностью, а той, какая получится реально (всё это и подразумевалось в статье Ромера), - можно для предварительной оценки вообще пренебречь полем снаружи длинного соленоида. Для поля же внутри длинного соленоида приближённо применима та же формула, что и внутри бесконечно длинного соленоида; в системе СИ это

где

Тогда таким путём оцениваемая интересующая нас величина есть


Получился ответ, как у автора статьи. Поскольку для

и

здесь были применены формулы поля бесконечно длинного соленоида, то естественно назвать это оценкой в приближении бесконечно длинного соленоида. Для второго, вдвое большего сопротивления аналогичная оценка есть

Вместо предсказанных так значений эксперимент дал соответственно

и

Поэтому автор и написал, что предсказание подтвердилось с точностью

% (поскольку

Таким образом, приближение (предельно простое по сравнению с громоздкими точными формулами и тем самым предпочтительное!) поля бесконечно длинного соленоида для предварительной оценки ожидаемых результатов опыта оказалось оправданным.
Притом, основная цель той статьи и той темы форума заключалась вовсе не в проверке применимости модели бесконечно длинного соленоида. Поэтому утверждения о противоречивости модели бесконечно длинного соленоида являются для той темы оффтопиком и затемняют там ясный основной сюжет.