ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ФЕРМА НА ЭЛЕМЕНТАРНОМ УРОВНЕ.
Итог 45-и летней работы над теоремой Ферма.
"Любое число считается целым пока не доказано иное".
"Все математики доказывают о безуспешных попытках осилить теорему ФЕРМА элементарными методами, забывая о 4-й степени, которая была доказана самим Ферма, не владеющим современным математическим аппаратом".
Допускаем, что уравнение Ферма

имеет решение в целых числах, а

есть его решение. Пусть здесь четным будет

В 80-х годах были получены формулы для решения уравнения (1), которые удовлетворяли условиям Ферма и первому случаю и второму. Формулы для простых степеней, их вывод были опубликованы на научном форуме dxdy. Вторая степень так же простое число, то действительно формулы обязаны подходить и для второй степени. И это так, мы не рассматривая отдельно уравнение второй степени, получили формулы для его решения. Новые формулы отличные от ранее известных, но формулы работают.
И так, если бы уравнение (1) имело решение в целых числах, то тройка чисел для его решения имела бы вид :



Здесь принято

делится на степень





Формулы для

и

опубликованы ранее на форуме dxdy.
Видим, что в формулах для

присутствуют символы

Поэтому зададимся вопросом : а из за какого или каких символов нет решения уравнения (1) в целых числах. Символы

есть во всех формулах для всех степеней, но 2-я степень имеет решение, это значит, что причина не в

. Но символа

нет в формулах для 2 и 3 степеней, но 2-я имеет решение и вывод : дело не в символе

А символ
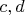
есть только в формулах для простых степеней, но нет в формулах для 2-й степени, а 2-я степень есть простое число.
Простое число : это число, которое делится само на себя и на единицу (например 2, 3, 5, 7 и т.д.). Вывод : символы
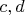
оказывает большое влияние на решаемость уравнений для простых степеней в целых числах. И мы докажем, что это обосновано. Доказывать будем, используя геометрический смысл теоремы Ферма.
Геометрический смысл теоремы Ферма отображён на рис.1.

Пояснения к геометрическому смыслу теоремы Ферма.
Решение уравнения (1) находим целочисленные

как точку пересечения графика

( на рисунке прямая АС) с кривой
![$x=\sqrt[r]{z^r-y^r}.$ $x=\sqrt[r]{z^r-y^r}.$](https://dxdy-02.korotkov.co.uk/f/1/7/2/172c6c0a631d00aab58e82bcfefad98482.png)
На рисунке показана кривая для

это круг радиусом

Для всех других степеней это уже не четвертая часть круга, а эллипс и

для этих степеней отображается на линии ВЕ, это отрезок ВG.
На рисунке : EF=

и ВF=

а отрезок ВI=ВJ=


это

относится к второй степени. Для всех остальных простых степеней

это отрезок BR и точка R расположена между точками F и J.
Отрезок АВ=ВС=

Это самое главное и это для всех степеней, включая и 2-ю.

и имеет с каждым из

общие делители, а

взаимно простые числа.
В треугольнике ВDH обозначим угол В, как

Тогда


В треугольнике ВFE обозначим угол В, как



В треугольнике BHG угол B обозначим, как


В треугольнике НGE :



1. Найдем

Рассмотрим треугольник ВEF. По теореме Пифагора

и

но известно :

То есть

Мы знаем, что

число рациональное, вида :

Правая часть (2) делится на

так как

и

Поэтому и левая часть обязана разделиться на это произведение. Здесь и далее приняли, что

. В левой части

по определению, тогда

то есть

Почему знаменатель делится на 2 , так как в первом члене слева есть 2. И ещё придется принять, что

делится на

и более. Примем, что

то есть

Избавимся в (2) от

в знаменателе, умножив правую и левую части на

и запишется это все так :

Сократим правую и левую части на

и все запишется :

Как видим, левая и правая части имеют по одному четному члену и по одному нечетному и это говорит о том, что делимость на 2 соблюдена и

пришлось принимать из за 2-и в первом члене слева. А то, что

приняли, что бы второй слева член в (3) остался четным и поэтому в (3) имеем по одному четному члену справа и слева и так же и по одному нечетному. Больше так подробно не будем показывать работу с уравнениями.
И так, мы пока определили, что :

2. Найдем отрезок DH.
Рассмотрим прямоугольный треугольник ВDH, здесь искомый отрезок катет, а второй катет равен

и гипотенуза равна


Справа член целый и целый первый член слева по определению, значит и

целое число и после умножения правой и левой частей на 2, будем иметь два члена чётных и один нечетный и так же первый член слева и

и

то DH должен иметь вид :


3. Найдем отрезок HE.
DH+HE=

и, если отрезок DH=

то и отрезок HE будет равен :

Приводим без доказательства, оставляя это на право читателю проверить самому.
То есть имеем

Рассмотрим треугольник BHE и найдем

применив теорему косинусов.

раскрыв

и зная, что согласно (2)

найдем :

Сравнив (6) и (2), видим, что:

4. Находим

в треугольнике HGE, используя теорему синусов.


В (8)

так как сумма членов во второй скобке слева делится на 4, а справа первый член, что видим из (7), делится на

и имеет вид :

.
5. Находим

из треугольника BHG по теореме косинусов.


и раскроем sin и cos, получим :

Сократим в (9) второй член справа на

и умножим левую и правую части на

имеем :

В уравнении (10) видим, что

число целое и обязано разделиться на

, что было показано ещё в предыдущем абзаце. Разделим первый член слева на

. Но ввиду того, что правая часть делится только на

значит это доказывает, что мы были ранее правы, что

не целое, а становится целым в квадрате. Разделим правую и левую части (10) на

и запишем :

Заменим

согласно (5).
Зная из (4), что

и раскрыв скобки у

(11) запишем :

Правая часть делится ещё и на

поэтому на

делится и

. Тогда можем записать :

Треугольник HGE, по теореме синусов находим


Треугольник HGE, теорема синусов, найдем отношение сторон


В (14)

поэтому можем сократить в (14) правую часть и левую на

и на

, здесь и далее мы опустим делимость на степень, так как рассматриваем делимость на

И (14) запишется :

Здесь :

Из треугольника HGE найдем


Уравнение (17), с учётом (12) и если извлечь квадратный корень, то можно записать :

Зная из (16), что

Поэтому и

, тогда

можно записать :

Поэтому (18) можно сократить на

умножив левую и правую части на

и все запишется :

Из (20) находим, что

Уравнение (6), учитывая (19), и сократив на

, запишем :

Учитывая (21) можно сделать вывод, что в (22)

и зная, что

и что

, а

, то можем смело записать :

или

Сравнение (23) и (24) приводятся пока без доказательства.
Из (5) следует, учитывая делимость

или, что тоже

то :

Сравнение (25) возведем в квадрат и умножим на 2, получим сравнение :

Сравнивая (26) и (27) находим, что :

В (28) избавились от знаменателей, умножив правую и левую части на :

Разделим (28) на

и на

получим :

То есть видим, что уже для 13 степени в (29)

.
Сравнение (29) доказывает, что :

Поэтому

, а это приводит нас к выводу, что в (12) число

не целое и мы правильно поступили, приняв при рассмотрении сравнений

.
Случай, когда на степень делится

или

не рассматриваем по причине, что эти случаи не влияют на результат при исследовании сравнений, как и первый случай Ферма.
И так :

и значит требуется принять, что

число рациональное и имеет вид :

. Тогда в (12)

И ещё - если в (12) левая часть после деления на

становится не целой, тогда и в правой части сумма двух членов не целое число, но первый член справа число целое по назначению, а именно

целое число по условию теоремы, а

это числитель рационального числа

и это целое число по определению. Тогда не целое число это второй член

Но

число целое по условию теоремы, а

может быть не целым, но не может быть числом рациональным, так как в квадрате это целое число согласно (4). Поэтому остаётся признать что число

не целое. Принимаем, что

число рациональное вида :

И

Поэтому (7) запишется, если умножим правую и левую части на

:

Как видим в (27), если в правой части

, то левая часть разделится на

ввиду того, что

, поэтому

, так как в последнем члене правой части в (27)

.
Но тогда снова видим, что в (6) :

То есть имеет место :

Или что то же :

, но

Сократим левую и правую части на

и запишем :

, но

, тогда можем заменить

на

при этом не нарушаем знак сравнения (в меньшей части заменяем большее число на меньшее) и получим

что противоречит (28).
А это значит, что и при рациональных

уравнение (6) не разрешимо в целых числах. Тогда принимаем, что

числа иррациональные (если принять иррациональным одно число

то в (12) в правой части сумма двух членов будет целое число, а в левой части число не целое ). Отсюда можно сделать вывод : в (12) в левой части произведение целого

на иррациональное

дает нам число иррациональное, но и в правой части произведение целого числа

на иррациональное число

в итоге получим иррациональное. Но сумма иррациональных чисел не может нам дать целое число

и на основании этого либо

либо

числа не целые. Если принять не целым число

а это числитель рационального числа, то теорема была бы доказана ещё в начале. Поэтому остаётся признать, что не целым числом является

Теорема Ферма доказана на элементарном уровне.
Теперь мы сможем объяснить почему из всех простых степеней решение уравнения Ферма имеет только 2-я степень. (2- число простое, делится только на 1 и на само себя)
Все дело в разности

Так, для второй степени эта разность равна 0, а для всех остальных степеней доказано, что очень малое число и не делится на цело на

.