Задача 3 из Ширяев, Вероятность - I, гл.2, §7 (Условные вероятность и матожидани).
Почему-то не включена в задачник Ширяев-Эрлих-Яськов. К тому же с опечатками.
Задача. Предположим, что случайные элементы
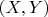
таковы, что существует регулярное распределение

Показать, что если

, то
![$$\mathsf{E}[g(X,Y)|X=x] = \int g(x,y)P_x(dy)\quad P_x\text{-п.н.} \qquad (1)$$ $$\mathsf{E}[g(X,Y)|X=x] = \int g(x,y)P_x(dy)\quad P_x\text{-п.н.} \qquad (1)$$](https://dxdy-02.korotkov.co.uk/f/d/3/e/d3ebcfbe5607fee99abc1674221dd9ee82.png)
(опечатка:

-п.н в (1) надо скорее всего понимать как

-п.н.).
Решение. Переобозначу

и пусть

- измеримые пространства.
Случайные элементы

и

являются соответственно

- и

-измеримыми и принимают значения в

и

.
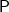
- вероятностная мера на

;

- распределение

:

;

- распределение
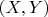
:

где

. На "прямоугольниках"

,

Пусть

-

-подалгебра

,

Для любого


По определению
![$\mathsf{E}[g(X,Y)|X=x]$ $\mathsf{E}[g(X,Y)|X=x]$](https://dxdy-01.korotkov.co.uk/f/8/f/0/8f0b9653d79be986d793ef99fc1fe2c182.png)
есть такая

-измеримая функция от

, что для каждого


где существование правого интеграла для каждого

гарантируется условием

, а существование
![$\mathsf{E}[g(X,Y)|X=x]$ $\mathsf{E}[g(X,Y)|X=x]$](https://dxdy-01.korotkov.co.uk/f/8/f/0/8f0b9653d79be986d793ef99fc1fe2c182.png)
- теоремой Радона-Никодима.
Поэтому утверждение задачи равносильно утверждению

Сначала проверяется для

, где

- "прямоугольник" из

. Если верно для

, то верно и для

, т.к.

(сумма конечная). Но тогда верно и для

, где

- верхний или нижний предел последовательности "элементарных множеств", т.е. множеств, состоящих из конечных сумм прямоугольников. Элементарными множествами и пределами их последовательностей исчерпывается

-алгебра

(что по-хорошему надо еще доказать). То есть утверждение верно для индикатора любого множества из

и, значит, для любой простой функции и функции, являющейся пределом последовательности простых.