Здравствуйте. Я переписал Доказательство с учётом замечаний в данной теме. Ещё 200 лет назад кто-то совершенно правильно заметил, что надо разделить доказательство на 2 случая: тройка чисел не делится и делится на показатель степени. Сначала я решил рассмотреть случай, когда одно из чисел тройки делится на показатель степени. Пусть это будет

. Чтобы было легче проверять доказательство, имеет смысл расписать его для показателя семь. Итак, имеем уравнение
![$x^7+y^7=z^7,z\equiv 0\bmod 7; \eqno [1]$ $x^7+y^7=z^7,z\equiv 0\bmod 7; \eqno [1]$](https://dxdy-02.korotkov.co.uk/f/d/4/a/d4a09c0340b483cd661d7e29e82a141882.png)
. Нужно доказать, что оно не имеет решений в натуральных попарно взаимно простых числах.
Идея в том, чтобы изготовить соотношения для  такие, что при подстановке их в
такие, что при подстановке их в ![$\eqno[1]$ $\eqno[1]$](https://dxdy-03.korotkov.co.uk/f/6/3/c/63c654e68d425ab5a401b20e3c46e8e282.png) получалось бы ТОЖДЕСТВЕННОЕ РАВЕНСТВО, либо близкое к тождественному!Доказательство Этап 1. С помощью формул Абеля получить соотношения для гипотетических решений уравнения
получалось бы ТОЖДЕСТВЕННОЕ РАВЕНСТВО, либо близкое к тождественному!Доказательство Этап 1. С помощью формул Абеля получить соотношения для гипотетических решений уравнения ![$\eqno[1]$ $\eqno[1]$](https://dxdy-03.korotkov.co.uk/f/6/3/c/63c654e68d425ab5a401b20e3c46e8e282.png) в натуральных попарно взаимно простых числах!
в натуральных попарно взаимно простых числах!Как и для кубов, доказывается от противного. Пусть существуют такие натуральные попарно взаимно простые числа

, что указанное равенство выполняется. Тогда, как и для кубов, справедлива лемма, правда имеющая некоторые отличия.
Лемма 1.Пусть уравнение

имеет решения в натуральных попарно взаимно простых числах для случая

делится на семь. Тогда верно следующее:
![$$\left\{
\begin{array}{lcl}
y=m^7+7p, \\
x=w^7+7p, \\
z=m^7+7p+w^7,m,w,C,D\in\mathbb{N},\ \eqno[2] \\
z=7C(7^5C^6-mwD),\\
p=mwA,\\
A=CD,7\mid C,\\
x+y=7^6C^7,\\
(C,D)=(y,D)=(x,D)=(m,C)=(w,C)=(m,w)=1
\end{array}
\right$$ $$\left\{
\begin{array}{lcl}
y=m^7+7p, \\
x=w^7+7p, \\
z=m^7+7p+w^7,m,w,C,D\in\mathbb{N},\ \eqno[2] \\
z=7C(7^5C^6-mwD),\\
p=mwA,\\
A=CD,7\mid C,\\
x+y=7^6C^7,\\
(C,D)=(y,D)=(x,D)=(m,C)=(w,C)=(m,w)=1
\end{array}
\right$$](https://dxdy-02.korotkov.co.uk/f/9/d/d/9ddcddd02e33953f5df444e9abdbb71882.png)
Доказательство леммы под спойлером
(Оффтоп)
Доказательство леммы.Как в знаменитой телеграмме, переносим

в правую часть, затем по аналогии

, при этом помня, что рассматривается случай

делится на семь. Тогда

 mihaild
mihaild показал, что

являются точными степенями. Вот его доказательство
Да, доказательство есть у Постникова ("Теорема Ферма", стр. 19-21 в издании 1978 года). Чтобы не потерялось, перепишу сюда.
Пусть

,

простое большее

,

взаимно просты,

не делится на

. Тогда
![$\sqrt[n]{z - x}$ $\sqrt[n]{z - x}$](https://dxdy-02.korotkov.co.uk/f/9/a/1/9a15b056a48386727db6e108ca2742c682.png)
- целое число.
Напишем

,

.
Очевидно что

и

взаимно просты, потому что любой их общий делитель делит

.
В выражении для

все слагаемые, кроме, быть может, последнего, делятся на

- значит любой общий делитель

и

делит

. Но у

нет общих делителей с

, а т.к.

не делится на

, то

тоже не входит в общие делители

и

. Значит,

и

взаимно просты. Ну и т.к. их произведение является

-й степенью, то и каждое из них является

-й степенью.
Рассуждение в общем-то довольно очевидное, я его кучу раз проводил, и каждый раз забывал не только доказательство, но и утверждение.

, то есть

Так как

Очевидно, если вспомнить определения чисел

чуть выше, то получится

. Получается, что

. Где
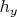
целое число.
Из определения

и произведенной ранее замены

следует

Так как

. Очевидно,

. Получается, что

. Где

целое число.

. Окончательно получаем

Пусть

делится на

. Тогда


. Поясню последний переход подробнее. Очевидно

Тогда

Надо ещё выяснить, могут ли

иметь какие-то общие делители. Прежде всего, нужно выяснить, чему вообще равно

. Делается это просто. В силу доказанного выше в лемме 1, записываем тождество

как


.
Решаем это уравнение относительно

в wolfram mathematica с помощью команды
Код:
Eq=(x+y-z)^7-7(x+y)(z-x)(z-y)D^7
Solve[Eq==0,D]
, нажимая shift enter и получаем, что


. Можно так же решить это уравнение с помощью wolfram alpha, правда корень он записывает в другом виде. Вот
ссылкаОтсюда следует, что

нечетно всегда: и когда

четное, и когда

нечетное. При таком раскладе получается, что

не может делиться на

в силу того, что

. Предположим, что

. Тогда

. Но ранее было установлено, что

. Получается, что

. Имеем противоречие, так как

. Имеем, что

.
Аналогично проверяется, что

.


.
Лемма доказана! Этап 2. Вывести такие соотношения для  что при их подстановке в
что при их подстановке в ![$\eqno[1]$ $\eqno[1]$](https://dxdy-03.korotkov.co.uk/f/6/3/c/63c654e68d425ab5a401b20e3c46e8e282.png) получалось бы тождественное равенство!Лемма 2
получалось бы тождественное равенство!Лемма 2. Существуют такие попарно взаимно простые натуральные числа

, что имеют место следующие соотношения, причём знаки согласованы!
![$$\left\{
\begin{array}{lcl}
x=\frac{a\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
y=\frac{a\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \ \ \eqno[3]\\
z=\sqrt[6]{7a}b,(a,b)=1,a,b,D,F\in\mathbb{N}\\
C=\frac{\sqrt[6]{7a}}{7},b=a-FD,F=mw\\
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl}
x=\frac{a\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
y=\frac{a\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \ \ \eqno[3]\\
z=\sqrt[6]{7a}b,(a,b)=1,a,b,D,F\in\mathbb{N}\\
C=\frac{\sqrt[6]{7a}}{7},b=a-FD,F=mw\\
\end{array}
\right.$$](https://dxdy-02.korotkov.co.uk/f/9/0/5/905e14c8e69d269d3d24a5f8aa89517382.png) Доказательство леммы 2
Доказательство леммы 2Вот далее совершенно неочевидный шаг, но такой же, как в доказательстве для кубов. Запишем тождество

. Вот доказательство того, что оно записано правильно
ссылка Конкретно для показателя семь вывод тождества под спойлером.(Оффтоп)
Самое простое - деление уголком по школьному. Как возникла идея записать такое тождество? Из за замены

Итак, как и для кубов, делаем замену

тогда

. В таком случае исходное уравнение принимает вид такой

. Получилось алгебраическое уравнение шестой степени относительно

, свободный член которого имеет должен быть целым. С помощью соотношений из леммы 1, имеем

и тогда свободный член переписывается следующим образом

. Вот и получилось то самое число, из которого тождество взялось. Далее деление уголком хоть по школьному
Умножим обе части тождества на

. Получим

. В силу доказанной леммы 1, в левой части тождества целое число, значит и последнее слагаемое в тождестве является целым числом. Доказательство под спойлером
(Оффтоп)
А почему в левой части тождества получается целое число? Вот берём соотношения из леммы 1
![$$\left\{
\begin{array}{lcl}
y=m^7+7p, \\
x=w^7+7p, \\
z=m^7+7p+w^7,m,w,C,D\in\mathbb{N},\ \eqno[2] \\
z=7C(7^5C^6-mwD),\\
p=mwA,\\
A=CD,7\mid C,\\
x+y=7^6C^7,\\
(C,D)=(y,D)=(x,D)=(m,C)=(w,C)=(m,w)=1
\end{array}
\right$$ $$\left\{
\begin{array}{lcl}
y=m^7+7p, \\
x=w^7+7p, \\
z=m^7+7p+w^7,m,w,C,D\in\mathbb{N},\ \eqno[2] \\
z=7C(7^5C^6-mwD),\\
p=mwA,\\
A=CD,7\mid C,\\
x+y=7^6C^7,\\
(C,D)=(y,D)=(x,D)=(m,C)=(w,C)=(m,w)=1
\end{array}
\right$$](https://dxdy-02.korotkov.co.uk/f/9/d/d/9ddcddd02e33953f5df444e9abdbb71882.png)
Сначала надо обратить внимание, что из первого, второго, третьего и пятого соотношений следует, что

! Затем смотрим на предпоследнее равенство и видим, что оказывается

, стало быть

. Теперь смотрим на пятое и шестое соотношения. Выясняется, что

Поэтому делаем замену переменной

и записываем

Важно понять, какой знак имеет число

. Выразим из последнего равенства

. Получается

. Вернёмся к равенству


Как видите, получилось квадратное уравнение относительно

. Посчитаем его дискриминант.

. Дискриминант представляет из себя в свою очередь квадратное уравнение такое

. Посчитаем его дискриминант.

Теперь решаем каждое квадратное уравнение

Ранее было получено, что

Получается ПТ

.
А дальше рассматриваем 2 случая:  нечетное и четное. Для начала пусть
нечетное и четное. Для начала пусть  четно, а
четно, а  нечетное.
нечетное. Нужно понять, четное или нечетное число

! Для этого, запишем величину

через

. Получится, что

. Но

нечетное число, так как

четное и по лемме 1, потому что

представляются в виде

умножить на целое нечетное число и

умножить на целое нечетное число. Тогда

также нечетные и Пифагорова тройка принимает вид следующий

![$\Rightarrow \left\{
\begin{array}{lcl}
z=\sqrt[6]{7ab}\\
m_0=-(a-b)^2 \\
p=\frac{a(a-b)}{(7(ab))^{5/6}}
\end{array}
\right.$ $\Rightarrow \left\{
\begin{array}{lcl}
z=\sqrt[6]{7ab}\\
m_0=-(a-b)^2 \\
p=\frac{a(a-b)}{(7(ab))^{5/6}}
\end{array}
\right.$](https://dxdy-02.korotkov.co.uk/f/9/b/1/9b161c112f93f6e33fdf3a82ae0d266682.png)
Важно понимать, что

могут не быть натуральными числами, поэтому

Здесь

является возможным общим делителем чисел в ПТ. Сейчас важно узнать, может ли

делиться на

. Для этого распишем

и узнаем, делится ли оно на семь.

.
В силу соотношений
![$\eqno[2]$ $\eqno[2]$](https://dxdy-02.korotkov.co.uk/f/1/3/7/1370d8bfb9aaf2485213813c6e54b0e682.png)
из леммы 1,

. Раз

не делится на

по лемме 1, то и

не делится и

не делится.
Запишем теперь

в терминах

.

Запишем дробь в терминах соотношений из леммы:

Эта дробь, которая на самом деле является натуральным числом, делится на

, причём не больше и не меньше. Запишем ее же в терминах

. Получим

Раз

делится на

по лемме 1, то

делится на

!
Как найти, чему равно  ?
? Через соотношение для неизвестной

. В терминах

она записывается следующим образом
![$p=\frac{(a-b)\sqrt[6]{7ab}}{7b}=\frac{(a_1-b_1)\sqrt[6]{7a_1b_1\alpha}}{7b_1}; p\in\mathbb{N}\Rightarrow \frac{7a_1\alpha}{b_1^5}\in\mathbb{N}\Rightarrow \alpha=b_1^5 \alpha_2;$ $p=\frac{(a-b)\sqrt[6]{7ab}}{7b}=\frac{(a_1-b_1)\sqrt[6]{7a_1b_1\alpha}}{7b_1}; p\in\mathbb{N}\Rightarrow \frac{7a_1\alpha}{b_1^5}\in\mathbb{N}\Rightarrow \alpha=b_1^5 \alpha_2;$](https://dxdy-01.korotkov.co.uk/f/4/1/3/41325afb08e1688806de263807ae003582.png) Теперь возникает вопрос, как найти
Теперь возникает вопрос, как найти  ?
? Используя факт, что числа

и

являются взаимно простыми в силу леммы 1!

Из леммы 1 следует, что

. Запишем

через

. Получим
![$z+7p=\frac{a_1\sqrt[6]{7a_1b_1^6\alpha_2}}{b_1}=a_1\sqrt[6]{7a_1\alpha_2}$ $z+7p=\frac{a_1\sqrt[6]{7a_1b_1^6\alpha_2}}{b_1}=a_1\sqrt[6]{7a_1\alpha_2}$](https://dxdy-04.korotkov.co.uk/f/3/4/7/347355e20143efc02545f656ce40efb482.png)
. Как уже было показано выше,

, значит

Осталось записать соотношения для

в окончательном виде!
Имеем
![$\left\{
\begin{array}{lcl}
z=\sqrt[6]{7a_1}b_1\\
p=\sqrt[6]{7a_1}\frac{a_1-b_1}{7} \\
(a_1,b_1)=1,a_1,b_1\in \mathbb{N}
\end{array}
\right.$ $\left\{
\begin{array}{lcl}
z=\sqrt[6]{7a_1}b_1\\
p=\sqrt[6]{7a_1}\frac{a_1-b_1}{7} \\
(a_1,b_1)=1,a_1,b_1\in \mathbb{N}
\end{array}
\right.$](https://dxdy-03.korotkov.co.uk/f/e/8/7/e8723a80aac2427f370ac605aacb7a2f82.png)
Далее индексы у  можно опустить и писать просто
можно опустить и писать просто  !
!Зная

и

можно найти

. Надо просто записать сумму и произведение

через

и найти

как корни квадратного уравнения. Произведение записывается через соотношение для

,а сумма - через соотношение для

. Я напомню, что в лемме 1 было доказано, что

. Ну и произведение

Осталось выразить

через

и можно решать квадратное уравнение. Из леммы 1, а также полученных соотношений для

, которые имеют вид
Цитата:
следует, что
![$x+y=7^6C^7\Rightarrow z+7p=7^6C^7\Rightarrow 7C=\sqrt[6]{7a}\Rightarrow C=\frac{\sqrt[6]{7a}}{7};\eqno[2.1]$ $x+y=7^6C^7\Rightarrow z+7p=7^6C^7\Rightarrow 7C=\sqrt[6]{7a}\Rightarrow C=\frac{\sqrt[6]{7a}}{7};\eqno[2.1]$](https://dxdy-04.korotkov.co.uk/f/b/5/a/b5a389c4f66c9d1bdfd65312f3f4da5982.png)
Получаем систему уравнений
![$$\left\{
\begin{array}{lcl}
m^7w^7=(a-b)^7D^{-7} \\
m^7+w^7=(2b-a)\sqrt[6]{7a}\ \eqno[2.2]\\
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl}
m^7w^7=(a-b)^7D^{-7} \\
m^7+w^7=(2b-a)\sqrt[6]{7a}\ \eqno[2.2]\\
\end{array}
\right.$$](https://dxdy-02.korotkov.co.uk/f/9/1/7/9175008b409f663845d7754f0ab1e9d682.png)
Находим

как корни квадратного уравнения с помощью теоремы Виета. Результат такой (знаки согласованы, это важно!!!)
![$$\left\{
\begin{array}{rcl}
m^7=\frac{(2b-a)\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
w^7=\frac{(2b-a)\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
\end{array}
\right.$$ $$\left\{
\begin{array}{rcl}
m^7=\frac{(2b-a)\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
w^7=\frac{(2b-a)\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
\end{array}
\right.$$](https://dxdy-04.korotkov.co.uk/f/b/3/f/b3f58ac0b14aadffaa6038d2be1eba5b82.png)
Раз теперь

известны, можно найти

с помощью соотношений из леммы 1, а также полученных соотношений для

, которые имеют вид
Цитата:
![$\left\{
\begin{array}{lcl}
x=w^7+7p \\
y=m^7+7p\\
p=mwA
\end{array}
\right.\Rightarrow \left\{
\begin{array}{lcl}
x=\frac{a\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
y=\frac{a\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \ \ \eqno[3]\\
z=\sqrt[6]{7a}b,(a,b)=1,a,b,D\in\mathbb{N}\\
\end{array}
\right. $ $\left\{
\begin{array}{lcl}
x=w^7+7p \\
y=m^7+7p\\
p=mwA
\end{array}
\right.\Rightarrow \left\{
\begin{array}{lcl}
x=\frac{a\sqrt[6]{7a}\pm\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \\
y=\frac{a\sqrt[6]{7a}\mp\sqrt{(2b-a)^2\sqrt[3]{7a}-4(a-b)^7D^{-7}}}{2} \ \ \eqno[3]\\
z=\sqrt[6]{7a}b,(a,b)=1,a,b,D\in\mathbb{N}\\
\end{array}
\right. $](https://dxdy-01.korotkov.co.uk/f/8/8/5/885022439d37114ee106427d792c8c6e82.png)
Знаки опять же согласованы!
Пусть по определению 
Осталось записать

через

! Получится, что

, что следует из двух способов представления числа

через

и

и соотношений
![$\eqno[2.1]$ $\eqno[2.1]$](https://dxdy-03.korotkov.co.uk/f/e/3/1/e317be0f5699d3fb5e460ae55e14507282.png)
, то есть нужны соотношения
![$\eqno[3],[2],[2.1]$ $\eqno[3],[2],[2.1]$](https://dxdy-01.korotkov.co.uk/f/8/3/3/833585a23695b7ac50bf3451085f3c9582.png)
из которых следует, что
![$z=\sqrt[6]{7a}b=7C(7^5C^6-mwD)\Rightarrow b=a-FD$ $z=\sqrt[6]{7a}b=7C(7^5C^6-mwD)\Rightarrow b=a-FD$](https://dxdy-02.korotkov.co.uk/f/9/3/e/93e92692bd18e9382024ba90a16abb9482.png)
и что числа

попарно взаимно простые, потому что

попарно взаимно простые по лемме 1!
Лемма 2 доказана Продолжение в следующем сообщении!