Пентадекатлон мечты

[EUgeneUS]

Dmitriy40 в сообщении #1704115 писал(а):

А теперь вопрос: а сколько кругов надо сделать чтобы найти решение? Про М48n21 не знаю, а вот для M12n15 прикинуть можно:
первый поиск проверил не менее 66387422053662391209161093722597723545 / 440538835723387181869888800 = 1.5е11 кандидатов для каждого из 46080 паттерна;
второй (или какой он там был по счёту) поиск проверил 80215613469168729088982885848674841 / 321796081609486619335200 = 2.45e11 кандидатов для каждого из 46080 паттерна;
итого было проверено не менее 46080*(1.5e11+2.45e11)=1.8e16 кандидатов (на самом деле в несколько раз больше, были и другие поиски).

Если ищем М48n21 то количество проверок нужно сравнивать не с количеством проверок для пентадекатлона, а с количеством проверок, выполненных уважаемым VAL для поиска М48n20. Или с количеством проверок при неудачном поиске М48n21.
Пусть таких проверок было $M$ (M - много )

Есть обоснованная надежда, что если выполнить такое же по порядку величины количество проверок, но не на 50 шаблонах, а на миллионах "примерно одинаково хороших" шаблонов, то М48n21 и найдётся.

Обоснование следующее.
Пока делаем $M$ проверок на миллионе (для определенности) шаблонов без увеличения порядка $N$ в районе $N_0$ (то есть $M$ - порядка миллиона или нескольких миллионов).
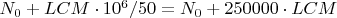
поверка по 50 шаблонам унесет $N$ до $N_0 + LCM \cdot 10^6 /50 = N_0 + 250000 \cdot LCM$, а LCM тоже огромный.

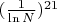
А падение вероятности найти цепочку в одной проверке с ростом $N$, как $(\frac{1}{\ln N})^{21}$, убивает всю надежду.

-- 01.10.2025, 21:35 --

Dmitriy40 в сообщении #1704115 писал(а):

Если хотите, могу сделать такую программу, на базе хоть 3-х, хоть 9-ти (ожидаю что он будет выгоднее) цифирного паттерна M48n21, но только одного, не десятков тысяч штук конечно, т.е. основные простые перераставлять не будет, только дополнительные. Даже самому интересно какова будет её скорость, насколько меньше той что без перебора простых в квадратах ...

Перестановка дополнительных (необязательных) простых даёт уже треть миллиона. И это хорошо.
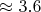
И хорошо бы сразу добавить $61$ в набор необязательных простых для квадратов. Это несильно увеличит LCM, а количество паттернов увеличит в 10 раз, то есть до $\approx 3.6$ миллиона.

"на базе хоть 3-х, хоть 9-ти (ожидаю что он будет выгоднее) цифирного паттерна" - не очень понял термин
Паттерн должен минимизировать количество неизвестных $p$, потом количество неизвестных $pq$ и т.д.

Ещё желательно сделать такое:
1. Проверку позиций от 1 до 19 проводить в порядке вероятности быстро найти негативный результат. Если результат негативный - другие позиции не проверять.

2. Проверку позиций 0 и 20 проводить, только если в позициях от 1 до 19 - успех.

Это позволит найти (и улучшить) цепочки длиной 19 и 20.

-- 01.10.2025, 21:40 --

Скорость перебора будет примерно такой же, если не учитывать увеличение времени на факторизацию с ростом $N$.
UPD: или даже может оказаться меньше, с учётом накладных расходов, про которые Вы написали выше.
А вот кандидатов такое должно находить больше за единицу времени.

-- 01.10.2025, 21:48 --

EUgeneUS в сообщении #1704119 писал(а):

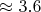
И хорошо бы сразу добавить $61$ в набор необязательных простых для квадратов. Это несильно увеличит LCM, а количество паттернов увеличит в 10 раз, то есть до $\approx 3.6$ миллиона.

Тут дополнение

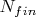
$61$ можно ставить на место любого необязательного простого в квадрате. Но поиск вести по всем паттернам до фиксированного задаваемого значения $N_{fin}$. Тогда увеличение LCM роли не играет. Ну, по некоторым вариантам паттернов проверок будет меньше, чем по другим. Но вероятность найти цепочку в каждой проверке будет примерно одинакова.

-- 01.10.2025, 21:57 --

И есть простой критерий, что метода сработала.
М48n21 найдётся после нескольких десятков М48n20.

Если на одном компе в 1..4..8 потоков за 10-15 дней будет находиться хотя бы одна цепочка М48n20, то можно собирать мощности заинтересованных людей, чтобы найти М48n21 за разумное время.
А если нет, то - нет.

[VAL]

Dmitriy40 в сообщении #1704115 писал(а):

Если хотите, могу сделать такую программу, на базе хоть 3-х, хоть 9-ти (ожидаю что он будет выгоднее) цифирного паттерна M48n21

Объясните, пожалуйста, как Вы собираетесь делать поиск 21-ки для $k=48$ на 9 простых. Вы уже писали об этом, но в качестве примера привели паттерн на 31 число. Насколько я понимаю, на 21-ку такого без упоминавшихся костылей не соорудить. Иное дела 21-ка или даже 19-ка по 24 делителя.

[Dmitriy40]

VAL в сообщении #1704122 писал(а):

Объясните, пожалуйста, как Вы собираетесь делать поиск 21-ки для $k=48$ на 9 простых.

Используя Ваш шаблон (который правда ещё не смотрел):

VAL в сообщении #1704100 писал(а):

Поколдовал над таблицей для 19-ки по 24 делителя для ускорителей. Удалось впихнуть 9 позиций, где оставшийся множитель обязан быть простым,

Упс, он для М24, ну не углядел, сорри. Значит 9 чисел для М48n21 пока в пролёте.

VAL в сообщении #1704122 писал(а):

Вы уже писали об этом, но в качестве примера привели паттерн на 31 число.

И сразу указал что можно обрезать и получить длину 24. Правда проверяемых мест всего 7, не 9, но и не 3 ведь.

В общем про 9 проверяемых мест для М48n21 я ошибся.

-- 01.10.2025, 23:21 --

EUgeneUS в сообщении #1704119 писал(а):

с количеством проверок, выполненных уважаемым VAL для поиска М48n20

Это легко прикинуть (для одного паттерна): 17668887847524548413038893976018715843277693308027547 / 3234 / 15763313547330727349557157245556968800 = 3.5e11. Три десятка разных паттернов дадут 1e13. В общем порядок не сильно отличается от M12n15 (и хуже так как числа заметно больше и их больше штук).

Кстати, до оптимизаций время на 10млн кандидатов у меня было 1 минута, значит 3.5e11 проверились бы за 3.5e11/1e7=35000 минут или 24 дня в один поток. Если угадать с паттерном ...

Разумеется поиск в низинах выгоднее. Вопрос выгоднее ли он на величину накладных расходов по генерации паттернов (и компиляции если она используется).

EUgeneUS в сообщении #1704119 писал(а):

"на базе хоть 3-х, хоть 9-ти (ожидаю что он будет выгоднее) цифирного паттерна" - не очень понял термин

Мне показалось (потому что не вникал, даже и не смотрел их) что VAL сделал два паттерна для M48n21, с тремя и девятью проверяемыми местами. Про 9 я ошибся, сорри.

EUgeneUS в сообщении #1704119 писал(а):

Проверку позиций 0 и 20 проводить, только если в позициях от 1 до 19 - успех.

Если на краях будет проверяемое число, как в выложенной программе M48n20 - отказ от его проверки в первую очередь несколько замедлит счёт. Конкретно для M48n20 - с 41с до 44с на 10млн кандидатов. При этом коэффициент фильтрации хуже в 11 раз, вместо 1139 будет 12415. Но благодаря отличной фильтрации до этого даже десятикратное увеличение объёма проверок на скорость влияет мало.


PS. Намёков не понимаю, пока не скажете прямо какую программу сделать никакую делать скорее всего не буду.

[VAL]

Dmitriy40 в сообщении #1704127 писал(а):

PS. Намёков не понимаю, пока не скажете прямо какую программу сделать никакую делать скорее всего не буду.

Кто я такой, чтобы командовать?!

А если посоветовать , я бы начал с 19-ки по 24 делителя с 9-ю проверками на простоту (см. последнюю запощенную таблицу).
Абсолютного рекорда это не даст. Но в случае успеха будет обновлен результат для $k=24$.
А заодно станет ясно, реально ли двигаться в этом направлении для достижения абсолютного рекорда.

[Dmitriy40]

VAL
"PS" был для EUgeneUS. Он же хочет программу с перетасовкой дополнительных простых ...
У меня пока лень пересиливает интерес (к скорости на PARI, так то всё понятно).

[EUgeneUS]

Dmitriy40 в сообщении #1704127 писал(а):

PS. Намёков не понимаю, пока не скажете прямо какую программу сделать никакую делать скорее всего не буду.

Поступило предложение:

VAL в сообщении #1704133 писал(а):

я бы начал с 19-ки по 24 делителя с 9-ю проверками на простоту (см. последнюю запощенную таблицу).

Там 8 необязательных простых в квадрате. Это дает $8! = 40320$, плюс должен быть зеркальный шаблон - ещё столько же. Итого, 80640. Всего в два раза больше, чем при поиске пентадекатлона.
То есть особых сложностей с генерацией ускорителей из-за огромного количества шаблонов быть не должно. Нет, ведь?

Кроме того, в этом шаблоне для M24n19 используется интересная (но пока сомнительная для меня) идея: минимизировать количество $pq$ в пользу $p$ и $pqr$.

Поэтому моё текущее мнение такое: поиск M48n20 отложить в пользу поиска M24n19 с ускорителями для 9 проверяемых чисел.
Не найдём, так согреемся проверим идею с минимизацией количества $pq$ в пользу $p$. Это будет понятно довольно быстро - как много будет находить кандидатов за единицу времени.

[Yadryara]

По поводу того, паттерны с каким количеством одиночных простых перспективнее. С наименьшим. То есть с 3-мя.

Мы же уже немало считали вероятности, если угодно частотности, для 12 делителей. Без асмовской предпроверки (т.н. ускорителей) частотность

для $p$ была 0.05-0.06, для $pq$ — 0.24-0.25.

C асмом для $p$ — 0.18-0.19, для $pq$ — те же 0.24-0.25.

Не вижу причин чтобы эти цифры существенно изменились в более высокогорных условиях для 24 либо 48 делителей. Простые всё равно реже встречаются чем полупростые.

А то, сколько паттернов считать в низинах, решат разумеется практические тесты готовых программ.

Успехи попыток ускорения на сегодняшний день для D(48, 20):

Интервал             Консоль               PARI         Last(cons)
10   млн            44.8 sec           49.4 sec           32.8 sec
100  млн      7min, 19.0 sec     7min, 26.1 sec     5min, 17.4 sec

Как видим, если сравнивать мои консольные запуски, удалось достичь 38-процентного ускорения именно на PARI.

Полагаю, эти же идеи будут работать и для D(48, 21). Причём выигрыш в скорости, видимо, будет ещё больше. Пока не проверял, потому что продолжаю пробовать идеи.

[VAL]

Yadryara в сообщении #1704162 писал(а):

По поводу того, паттерны с каким количеством одиночных простых перспективнее. С наименьшим. То есть с 3-мя.

Мы же уже немало считали вероятности, если угодно частотности, для 12 делителей. Без асмовской предпроверки (т.н. ускорителей) частотность

для $p$ была 0.05-0.06, для $pq$ — 0.24-0.25.

C асмом для $p$ — 0.18-0.19, для $pq$ — те же 0.24-0.25.

Не вижу причин чтобы эти цифры существенно изменились в более высокогорных условиях для 24 либо 48 делителей. Простые всё равно реже встречаются чем полупростые.

То что $pq$ вероятнее $p$ известно, многократно обсуждалось и не подлежит сомнению. А вот то, что поиск длинной цепочки с ускорителями будет выгоднее для 3-х простых, чем для 9-и уже не очевидно.
Допустим (цифры условные) в первом варианте искомые цепочки встречаются в 10000 раз чаще, но во втором перебор в 100000 раз быстрее. Тогда какой вариант выгоднее?

[Yadryara]

VAL в сообщении #1704170 писал(а):

Допустим (цифры условные) в первом варианте искомые цепочки встречаются в 10000 раз чаще, но во втором перебор в 100000 раз быстрее. Тогда какой вариант выгоднее?

Сформулируйте более понятным языком, плиз. Что за первый вариант, что за 2-й.

На всякий случай: применение асма позволяет искать быстрее не только $p$, но и $pq$.

[Dmitriy40]

То что $p$ реже $pq$b $pqr$ понятно. Но зато проверка таких паттернов быстрее потому что isprime быстрее factor, тем более для больших чисел. И ускорители проверяли лишь места $p$, остальные ускорителями не проверялись никак оставляя всю работу PARI.
Будут ли на PARI быстрее 9шт $p$ чем 3шт $p$ - я не знаю. По идее должны бы, в силу именно time(isprime)<<time(factor), ведь при этом можно сильно реже запускать factor. Вопрос насколько реже и насколько менее вероятны 9шт $p$ относительно 3шт $p$, что пересилит в итоге.
Для ускорителей лучше больше простых - будет лучше фильтрация, меньше останется кандидатов в PARI для isprime и factor, и они будут быстрее пересылаться (тысячу строк переслать или сто миллионов - очень большая разница по времени).

EUgeneUS
А, так речь про ускорители, я то думал про PARI с перебором размещений перед перебором $p$, это же интереснее.

VAL
У меня технический вопрос по выложенной M48n20 (M48n21 не изучал): перебор идёт по $3234p$ на +7, а почему не по $360p$ на +13? Числа чуть меньше, проверяться будут капельку быстрее.

Yadryara в сообщении #1704180 писал(а):

На всякий случай: применение асма позволяет искать быстрее не только $p$, но и $pq$.

Это как?! Я не в курсе. И в ускорителях не применялось.
Обсуждалась добавка такой проверки, но реально было сделать лишь проверку делителей до скажем $10^6$ и если оных получится больше одного, то значит там точно не $pq$ и такого кандидата отвергаем. Но это невероятно и выигрыш не стоит усилий и замедления (ведь придётся для каждого не отвергнутого в итоге кандидата перебрать все делители для всех мест $pq$ либо исправлять внутренний цикл чтобы он не отвергал кандидатов сразу по нахождению делителя, а подсчитывал их количество и отвергал только при нахождении двух, причём только для некоторых мест из всех, это совсем геморно и тоже замедлит, ради мелкого выигрыша в фильтрации).

[Yadryara]

Dmitriy40 в сообщении #1704189 писал(а):

Это как?!

Для этого и использовано именно слово "позволяет". То есть позволяет в принципе.

Dmitriy40 в сообщении #1704189 писал(а):

Вопрос насколько реже и насколько менее вероятны 9шт $p$ относительно 3шт $p$,

Обратный логарифм 6-й степени, вестимо. То есть в случае 9 одиночных простых кандидаты будут быстро уходить всё выше в горы, что плохо.

В общем, если не лень, похоже придётся на практике сравнивать два варианта с крошечным количеством простых и большим. Хотя может и соседние сравнить: 3 и 4 простых.

[EUgeneUS]

Dmitriy40 в сообщении #1704189 писал(а):

А, так речь про ускорители, я то думал про PARI с перебором размещений перед перебором $p$, это же интереснее.

Есть\было два альтернативных предложения

1. Поискать M48n21 на миллионах паттернов (вместо 50) за счет перебора размещений необязательных простых в квадрате.
Это уже должно дать эффект, даже без ускорителей. А уж если ускорители можно сделать на эти миллионы паттернов, то будет вообще прекрасно...

2. Поискать M24n19 с ускорителями для 9 проверяемых чисел.
Это само по себе интересно - проверить идею минимизации количества $pq$ за счет максимизации количества $p$.

-- 02.10.2025, 13:33 --

Yadryara в сообщении #1704193 писал(а):

Обратный логарифм 6-й степени, вестимо.

Нет, конечно.
Поиск 6 простых не просто же отбрасывается, а заменяется поиском $pq, pqr..$
Если в шести позициях вместо $p$ ищем $pq$, то грубая оценка: $1/(\ln (\ln (N)))^6$

-- 02.10.2025, 13:36 --

Для 40-значных чисел, это примерно в 8500 раз.
Для 100-зачных чисел, это примерно в 26000 раз.

[Dmitriy40]

EUgeneUS в сообщении #1704199 писал(а):

1. Поискать M48n21 на миллионах паттернов (вместо 50) за счет перебора размещений необязательных простых в квадрате.
Это уже должно дать эффект, даже без ускорителей.

Мне интереснее этот вариант. Особенно с расширением списка дополнительных простых. И на PARI.
Вот только с чем сравнивать? Если для тестов, то удобнее взять выложенный вариант M48n20 с 8 местами для дополнительных простых, там известно сколько перебрано итераций по одному паттерну (выделенному, счастливому, удачному), 3.5e11, можно будет посмотреть сколько понадобится итераций по миллионам паттернов.


Кстати, стоит ли показать как на PARI вычислить константы для длинного if и для T[]? Чтобы не брать их "из ниоткуда или свыше", а встроить расчёт прямо в программу, это доли секунды. Как и p1 и m. Или это всем понятно и вопросов не вызывает?

[EUgeneUS]

Я правильно помню, что для M12n15 в шаблонах было 11 $p$ и 4 $pq$?

-- 02.10.2025, 14:54 --

Dmitriy40 в сообщении #1704209 писал(а):

Вот только с чем сравнивать? Если для тестов, то удобнее взять выложенный вариант M48n20 с 8 местами для дополнительных простых, там известно сколько перебрано итераций по одному паттерну (выделенному, счастливому, удачному), 3.5e11, можно будет посмотреть сколько понадобится итераций по миллионам паттернов.

Можно и так проверить идею.
А можно можно сразу сделать для M48n21, и посмотреть, как быстро находит кандидатов с 1-2 пропусками.
Из чего сделать вывод о перспективах дальнейшего расчета.
Как удобнее.

[Dmitriy40]

EUgeneUS в сообщении #1704210 писал(а):

Я правильно помню, что для M12n15 в шаблонах было 11 $p$ и 4 $pq$?

Да.