По построению оценки вероятности найти цепочку по паттерну.
Кратко:
Вероятности найти удачное число в каждом месте считаются независимыми.
Оцениваются так:
1. Известны функции
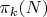
- (асимптотически) количество чисел, свободных от квадратов, с ровно

множителями. Берем от них производную по

- получаем плотности вероятности найти число с ровно

множителями для случайно выбранного N.
Обозначим их
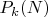
и назовём "базовыми" вероятностями.
2. В базовые вероятности нужно подставлять не само число

- в районе которого ищем цепочку, а число
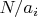
, где

произведение всех множителей, заданных шаблоном:
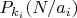
- базовая вероятность для i-го места в шаблоне.

- количество простых множителей:

, для

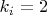
, для

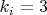
, для

и т.д.
3. Далее нужно рассчитать
поправочные коэффициенты к вероятностям. (Этот шаг был пропущен в прошлой оценке и именно в этом была ошибка).
Смысл этих коэффициентов в том, что применяя шаблоны, мы гарантируем, что ни одно неизвестное число
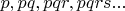
не делится на простые числа, которые используются в шаблоне.
Это факт изменяет базовые вероятности, причем разным образом - в зависимости от того, сколько множителей содержит неизвестное число.
а) для неизвестных простых. Все числа, которые "вычеркнуты" шаблоном - "плохие". Очевидно, если число делится на небольшое простое, оно не может быть большим простым

Тогда считаем долю оставшихся чисел, после "вычеркивания", как
в этом сообщении.
Обратное число и будет
поправочный коэффициент для вероятности найти простое, обозначим его

:
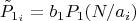
где
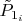
- уже "настоящая вероятность", найти на i-м месте неизвестное простое.
б) для неизвестных

. Точного расчета у меня нет. Приблизительный такой:
если число делится (как минимум) на два простых из шаблона, то оно уже не может быть большим

, доля таких чисел:
- считаем долю чисел, которые делятся на каждую пару:
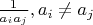
- потом суммируем. Отнимаем от единицы - это и будет поправочный коэффициент

:
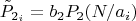
где
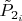
- уже оценка "настоящей вероятность", найти на i-м месте неизвестное

.
Про поправочные коэффициенты можно сказать, что они зависят от шаблона, но не от

.
4. После чего перемножаем вероятности для каждой позиции и получаем вероятность успеха при однократной проверке по данном шаблону в районе заданного

.
Далее расскажу, про применение этой модели к шаблону для пентадекатлона.
-- 04.10.2025, 21:13 --Вот, что получилось для взятого наугад шаблона для пентадекатлона:

Параметр модели - число

, тут


- произведения всех чисел в столбце шаблона
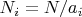
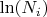
и
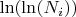
- используются для расчёта "базовых вероятностей"

Поправки к вероятностям рассчитывались, как описано выше.
Результат, оценка вероятности найти цепочку за один раз - строка 22 (

)
Видно, что вероятности для простых вроде бы похожи на правду. А вероятности для

выглядят заниженными, видимо из-за ошибки в расчете поправки для них....
 -- 04.10.2025, 21:19 --
-- 04.10.2025, 21:19 --Тут всё тоже самое, но для
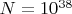
:

В общем,
1. Скорее всего имеются ошибки в расчете поправочных коэффициентов. Для

- точно имеются.
2. Скорее всего они устранимы.
3. Когда\если их устранить, то будет способ оценивать вероятность найти цепочку в заданной размерности при известном шаблоне.
4. Так как промежуточным результатом являются вероятности по каждой позиции шаблона - можно будет навешивать туда веса для оценки скорости вычислений и сравнения шаблонов уже по этому критерию.