Вот шустряк подвернулся...

Полагаю, это не случайно.
Вот, например, при поиске цепочки из 9 чисел для

именно "шустряк подвернулся". Кандидатуры, прошедшие предварительный отбор, появлялись очень редко. И я уже хотел было остановить отбор, когда одна из таких кандидатур неожиданно сработала, причем без долгих вычислений.
А для восьмерки чисел, имеющих по 11664 кандидаты появлялись с завидной регулярностью. Например, остановленное Вами 63473... тоже, скорее всего, дало бы требуемую цепочку. А еще за короткое время у меня набралось несколько пар, для которых при доходящем разложении каждого из чисел, нашлась бы искомая восьмерка.
Очевидно, это связано с каноническим разложением $k=2^4*3^6". С одной стороны, квадраты, используемые в шаблоне, не загоняют нас в какие-то совсем уж заоблачные числа, как это делали бы более высокие степени. А с другой, числа, остающиеся после отделения обязательных множителей, чаще всего имеют именно по 4 делителя. То есть макушка "колокола", о котором писал
vicvolf, приходится именно туда, куда надо. И это было заранее ясно. Единственное что удивило - этот колокол оказался весьма "крутым", даже случаи по 3 и 5 множителей встречаются значительно реже, чем четверки.
А еще вполне возможно, что легкость поиска обусловлена близостью среднего геометрического простых множителей 11664 к числу

.
-- 01 окт 2025, 10:41 --Максимально "хороший" набор неизвестных
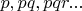
- это минимизация количества чисел с мЕньшим количеством простых множителей в пользу чисел с бОльшим количеством простых множителей.
Но для каких-то цепочек всё равно будут неизвестные простые

. И вот в этом случае использовать ускорители Дмитрия.
Три года назад мы эмпирически пришли к выводу, что оптимальный шаблон для писка длинных цепочек рассчитан на проверку на простоту трех чисел.
Но в такой ситуации ускорители Дмитрия мало что дают. Ну нашли мы триллион кандидатов, а теперь искать среди них те, где 18 оставшихся чисел разложатся как надо... Вариант для

тупиковый, поскольку наиболее вероятное разложение оставшихся чисел

или

, а нам надо массу

.
А вот шаблон на 9 простых может реально помочь (хотя может и не помочь, надо проверять). Без ускорителей мы будем сутки искать кандидатуру, проходящую отбор по простым. А если ускорим эту стадию, то останется 12 чисел, 6 из которых требуют разложения

, а другие 6 -

. Тоже не сахар, но в тысячи раз вероятнее, чем 18 чисел.
В общем надо пробовать. Возможно, сначала не для цепочки длиной 21, а хотя бы 19, что будет не абсолютным рекордом, а только рекордом для

.