Присоединяюсь. Вот например такое определение: точки
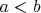
являются соседними, если не существует точки

такой, что

. Подойдёт ли оно? Если да, тогда можно назвать виновника сразу: плотность порядка вещественных чисел (которая как раз и утверждает ровно то, что соседних точек не существует). Но при этом если бы порядок не был бы ещё и линейным, могли бы например найтись такие точки

, что если что-то меньше/больше одной из них, то оно и меньше/больше и другой из них (это означает, что они не могли бы быть сравнимы друг с другом, то есть отрицает линейность порядка). Такие точки не так много смысла называть «соседними», но в принципе можно было бы — так что если принимать такое более общее определение (несравнимы, но одинаково сравнимы со всем остальным), то виновата не только плотность порядка, но и линейность.