Найти интеграл от дифференциальной формы по M^2, применяя те

[Juicer]

Здравствуйте!
Дано многообразие M^2 = $\{(x, y, z): x^2 + y^2 + z^2 = 4, x \leq z \}$ и нормаль $n_x(-2, 0, 0) > 0$ UPD: поправил нормаль, теперь это точка на сфере
Пытаюсь найти такой интеграл от дифференциальной формы: $\iint_{M^2}x^2dy \wedge dz + \cos x dx \wedge dz$, применяя теорему Стокса.
По теореме Стокса получим: $d(x^2dy \wedge dz + \cos x dx \wedge dz = 2x dx\wedge dy \wedge dz) + 0$.
Нашими условиями мы получим половину сферы. В координатах нормали х не равен z - значит, точка попадает в нашу полусферу.
Я взял параметризацию $(x, y, z) = (r \sin (u) \sin (v), r \cos (u), r \sin (u) \cos (v))$.
Поскольку вычислять нормаль нужно для точки сферы, я закрепил радиус $r = 2$ и находил нормаль, получается, к окружности. Находим вектор, перпендикулярный двум векторам, задающим параметризацию окружности. Это и будет вектор нормали.
Подставляем координаты в него из условия и смотрим выполнения условия, что в данной точке он положителен. Оно не выполняется - значит, нужно либо искать другую параметризацию, либо просто поставить знак "-" перед интегралом.
Я поставил просто знак "-".
Далее из полученного по теореме Стокса и нормали получаем, что искомый интеграл равен интегралу
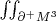
$- \iiint_{M^3} 2xdx\wedge dy\wedge dz$. Вот здесь получается, ещё нужно вычесть интеграл $\iint_{\partial^+M^3}$, но я не уверен в этом. Значение же трёхкратного интеграла получилось $4\sqrt{2} \pi$
Подскажите, пожалуйста, всё ли я правильно делаю, и нужно ли вычитать этот интеграл? И что вообще получится тогда под знаком этого интеграла, там ведь стоит $\cos (x)$ из начальных условий?

[DeBill]

Juicer
Ваша поверхность - полусфера.

Juicer в сообщении #1431868 писал(а):

применяя теорему Стокса

Так - можно, но следует отдавать себе отчетЮ что и зачем-как Вы делаете...
Например:

Juicer в сообщении #1431868 писал(а):

Я взял параметризацию

Зачем, если делаете "по Стоксу"? Где она там нужна?
И вообще: что дает формула Стокса (ну, тут его называют Гауссом-Остроградским, неважно). Какова же граница полушара? Как она должна быть ориентирована для Стокса? Та ли ориентация на полусфере получается, что в Вашей задаче? Прибавлять или вычитать интеграл по диску? Как он ориентирован? Как его считать (надо - его параметризацию...Будет ли (непостроенная еще ) она согласована с ориентацией диска? ).

[Juicer]

Дело в том, что этого и не понимаю.
Касаемо параметризации - она нужна потом, чтобы посчитать сам интеграл, да, сначала она не нужна.
Границу мы должны обходить так, чтобы она оставалась слева.
Не знаю, такая же ориентация получается, как и нужна.
Что делать с интегралом по диску тоже не знаю - это и есть основной вопрос.
Ориентирован положительно.
Считать - примем x = z, оттуда получим угол Pi/4, радиус равен от нуля до двух; в качестве V подставим Pi/4, получим выражения для x и у. Посчитаем двойной инттеграл

-- 25.12.2019, 15:47 --

Ну а вообще, я хотел бы избавиться от каши, которая сейчас в голове.
Поможете?

[Brukvalub]

Juicer в сообщении #1431874 писал(а):

Границу мы должны обходить так, чтобы она оставалась слева.

Звучит это странно.

Juicer в сообщении #1431874 писал(а):

Что делать с интегралом по диску тоже не знаю - это и есть основной вопрос.

Диск нужно сначала добавить к полусфере, чтобы получить ограниченное замкнутое многообразие, применить к нему ф-лу Стокса, затем вычесть из результата насильственно добавленный интеграл по диску.

[Juicer]

Brukvalub в сообщении #1431877 писал(а):

Звучит это странно.

Согласен, написал чушь.
Мы должны обходить область(диск у нас) по границе так, чтобы диск оставался по левую сторону от границы.

Brukvalub в сообщении #1431877 писал(а):

Диск нужно сначала добавить к полусфере

Правильно ли я понимаю, что, для того, чтобы это сделать, мы сначала просто меняем изначальное условие $x\leqz$ на $x <z$, потом находим интеграл?
Что мне нужно вычесть? Интеграл

$$\iint_{\partial^+ M^3}x^2dy \wedge dz + \cos x dx \wedge dz?$$

[Brukvalub]

Juicer в сообщении #1431878 писал(а):

Мы должны обходить область(диск у нас) по границе так, чтобы диск оставался по левую сторону от границы.

Juicer в сообщении #1431878 писал(а):

Согласен, написал чушь.

И снова чушь.

Juicer в сообщении #1431878 писал(а):

Что мне нужно вычесть?

Brukvalub в сообщении #1431877 писал(а):

вычесть из результата насильственно добавленный интеграл по диску.

[Juicer]

Brukvalub в сообщении #1431882 писал(а):

И снова чушь.

Поясните, почему.

Brukvalub в сообщении #1431882 писал(а):

вычесть из результата насильственно добавленный интеграл по диску.

Как составить этот интеграл? У меня же знак внешнего произведения и косинус.

[svv]

Juicer
Не хочу сбивать Вас с намеченного плана, но замечу на будущее.

Ко второму слагаемому теорему Стокса можно применить «наоборот», сведя интегрирование по полусфере $M$ к интегрированию по её границе $\partial M$, т.е. окружности:
$\int\limits_{M} \cos x\;dx \wedge dz = \int\limits_{M} d(\sin x\;dz) = \int\limits_{\partial M} \sin x\;dz$

С первым слагаемым так не получится. Форма $x^2\;dy\wedge dz$ не является дифференциалом другой формы. Но можно воспользоваться тем, что $x^2\;dy\wedge dz\stackrel{M}{=}(4-y^2-z^2)\;dy\wedge dz$ (то есть ограничения этих форм на $M$ совпадают).

[Brukvalub]

Juicer в сообщении #1431886 писал(а):

Поясните, почему.

По многим причинам. В частности, потому, что на диске изначально не задана никакая ориентация, поэтому пока бессмысленно обсуждать согласованность этой ориентации с ориентацией границы диска.

[Juicer]

svv,

svv в сообщении #1431887 писал(а):

Ко второму слагаемому теорему Стокса можно применить «наоборот»

Правильно ли я понимаю, что это мне пригодится для вычисления интеграла по диску? Ибо, применяя теорему стокса, мы получим произведение $dx \wedge dx$ и всё второе слагаемое занулится.
Brukvalub,

Brukvalub в сообщении #1431890 писал(а):

По многим причинам. В частности, потому, что на диске изначально не задана никакая ориентация, поэтому пока бессмысленно обсуждать согласованность этой ориентации с ориентацией границы диска.

Не понимаю, что вы хотите этим сказать.
Для диска возьмём стандартную параметризацию окружности $\begin{equation*}\begin{cases}x=r \cos (t), \\ y=r \sin (t), r \in (0, 2], t\in [0, 2\pi ]. \end{cases} \end{equation*}$
Здесь угол t будет равен углу u, который использовался мной для параметризации сферы.

[svv]

Juicer в сообщении #1431901 писал(а):

Правильно ли я понимаю, что это мне пригодится для вычисления интеграла по диску? Ибо, применяя теорему стокса, мы получим произведение $dx \wedge dx$ и всё второе слагаемое занулится.

Интеграл от второго слагаемого действительно нулевой, только я не совсем понял Вашу логику. (Она, возможно, совершенно правильная!)

Я рассуждал так. Мы применили теорему Стокса, получили интеграл от 1-формы $\sin x\;dz$ по $\partial M$, то есть по окружности. Однако $\partial M$ лежит в плоскости $x=z$, поэтому
$\sin x\;dz\stackrel{\partial M}{=}\sin x\;dx=d(-\cos x)$
Ну, а интеграл от этой штуки по $\partial M$, очевидно, нулевой.

А как Вы рассуждали?

[Juicer]

svv в сообщении #1431902 писал(а):

А как Вы рассуждали?

Вы имеете ввиду, как я получил ноль? По свойству $k$-форм, любая форма обращается в ноль при совпадении двух её аргументов. У нас получится при $d(\cos(x)dx\wedge dz) = \sin(x) dx \wedge dx \wedge dz$ два одинаковых аргумента - $dx \wedge dx.$

[svv]

Погодите, $d(\cos x \;dx\wedge dz)=0$ ещё не означает, что интеграл от $\cos x \;dx\wedge dz$ по любой поверхности равен нулю. Только по замкнутой. Также это позволяет заменить незамкнутую поверхность другой незамкнутой поверхностью, опирающейся на ту же границу (в нашем случае перейти от интеграла по полусфере к интегралу по диску, например). И?

[Juicer]

svv в сообщении #1431908 писал(а):

Погодите,

Я не утверждаю, что он нулевой по любой поверхности. Я лишь говорю, что, применяя теорему Стокса и переходя к многообразию $M^3$, это слагаемое будет равно нулю, соответственно, и интеграл тоже.
Я пытаюсь выяснить, какой диск получится(или как его получить). Я работаю в многообразии $M^3.$
Насколько я понял, вы предлагаете не переходить к $M^3$, а, применив теорему Стокса в обратную сторону, перейти от $M^2$ к интегрированию по $\partial^+M^2?$
Если это так, то я не понимаю, что делать с внешним произведением $dy \wedge dz$ - поскольку, как вы сами сказали, такая форма(ещё с $x^2$) не является дифференциалом другой формы. Ваше предложение о совпадении ограничений этих форм я не понял. Что это мне даст?

[svv]

Juicer в сообщении #1431911 писал(а):

Я лишь говорю, что, применяя теорему Стокса и переходя к многообразию $M^3$, это слагаемое будет равно нулю, соответственно, и интеграл тоже.

А как Вы примените теорему Стокса "в сторону увеличения размерности", если Ваша полусфера незамкнутая? Вы правы в том, что возникающий объёмный интеграл равен нулю. Но для применения теоремы Вам надо ещё дополнить полусферу до замкнутой поверхности. Например, диском. А тогда Вы просто заменяете один неизвестный интеграл (по полусфере) другим неизвестным интегралом (по диску), но не доказываете, что хоть один из них равен нулю.

Juicer в сообщении #1431911 писал(а):

Насколько я понял, вы предлагаете не переходить к $M^3$, а, применив теорему Стокса в обратную сторону, перейти от $M^2$ к интегрированию по $\partial^+M^2?$

Совершенно верно.

Juicer в сообщении #1431911 писал(а):

Если это так, то я не понимаю, что делать с внешним произведением $dy \wedge dz$ - поскольку, как вы сами сказали, такая форма(ещё с $x^2$) не является дифференциалом другой формы.

К первому слагаемому другой подход, давайте сначала разделаемся со вторым.